The value of 'a' for which the scaler triple product formed by the vectors \(\vec\alpha=\hat{i}+a\hat{j}+\hat{k}\), \(\vec{\beta}=\hat{j}+a\hat{k}\) and \(\vec{\gamma}=a\hat{i}+\hat{k}\) is maximum, is
- 3
- -3
- \(\frac{1}{\sqrt3}\)
- \(-\frac{1}{\sqrt3}\)
The Correct Option is D
Approach Solution - 1
\(\begin{vmatrix} 1 &a &1 \\ 0&1 &a \\ a& 0 &1 \end{vmatrix}\)
\(=1-a(-a^2)-a\)
\(=1+a^3-a\)
differentiating we get, \(\frac{\alpha v}{qa}=3a^2-1=0\)
\(q\equiv \frac{-1}{\sqrt3}\)
So, the correct option is (D) : \(\frac{-1}{\sqrt3}\)
Approach Solution -2
Given :
\(α=\hat{i}+a\hat{j}+\hat{k},β=0\hat{i}+\hat{j}+a\hat{k},γ=a\hat{i}+0\hat{j}+\hat{k}\)
\([α,β,γ]=\begin{vmatrix} 1 & a & 1 \\ 0 & 1 & a \\ a & 0 & 1 \end{vmatrix}\)
\(=1(1-0)-0+a(a^2-1)\)
\(=a^3-a+1=f(a)\) (let)
Now, for maximum scalar triple product,
\(f'(a)=0⇒3a^2-1=0\)
\(⇒a=\pm\frac{1}{\sqrt3}\)
Now, \(f''(a)=6a\)
\(⇒f''(\frac{1}{\sqrt3})\gt0,f''(\frac{-1}{\sqrt3})\lt0\)
Therefore, \(a=-\frac{1}{\sqrt3}\) is the point of maxima.
So, the correct option is (D) : \(\frac{-1}{\sqrt3}\)
Top Questions on Vector Algebra
- Let \(\vec{p}=2\hat{i}+\hat{j}+3\hat{k}\) and \(\vec{q}=\hat{i}-\hat{j}+\hat{k}\). If for some real numbers α, β and γ we have
\(15\hat{i}+10\hat{j}+6\hat{k}=α(2\vec{p}+\vec{q})+β(\vec{p}-2\vec{q})+γ(\vec{p}\times\vec{q})\),
then the value of γ is ________.- JEE Advanced - 2024
- Mathematics
- Vector Algebra
- Let \(\overrightarrow{OP}=\frac{\alpha-1}{\alpha}\hat{i}+\hat{j}+\hat{k},\overrightarrow{OQ}=\hat{i}+\frac{\beta-1}{\beta}\hat{j}+\hat{k}\) and \(\overrightarrow{OR}=\hat{i}+\hat{j}+\frac{1}{2}\hat{k}\) be three vector where α, β ∈ R - {0} and 0 denotes the origin. If \((\overrightarrow{OP}\times\overrightarrow{OQ}).\overrightarrow{OR}=0\) and the point (α, β, 2) lies on the plane 3x + 3y - z + l = 0, then the value of l is _______.
- JEE Advanced - 2024
- Mathematics
- Vector Algebra
- Given \(|\vec b=2, |\vec b\times \vec a|=2,\) then the value of \(|\vec b\times \vec a-\vec b|^2\) is
- JEE Main - 2024
- Mathematics
- Vector Algebra
- Let \(\vec a =3î + ĵ -2k̂\), \(\vec b =4 î + ĵ +7 k̂\) and \(\vec c =î -3 ĵ +4 k̂\) be 3 vectors. If a vector \(\vec p\) satisfies \(\vec p_x \vec b=\vec c_x\vec b\) and \(\vec p_x\vec a = 0\) then \(\vec p.( î - ĵ - k̂ )\) is equal to
- JEE Main - 2024
- Mathematics
- Vector Algebra
Let $\vec{u}=\hat{i}-\hat{j}-2 \hat{k}, \vec{v}=2 \hat{i}+\hat{j}-\hat{k}, \vec{v} \cdot \vec{w}=2$ and $\vec{v} \times \vec{w}=\vec{u}+\lambda \vec{v}$. Then $\vec{u} \cdot \vec{w}$ is equal to
- JEE Main - 2023
- Mathematics
- Vector Algebra
Questions Asked in WBJEE exam
- \(\lim_{x\rightarrow \infty}\){\(x-\sqrt[n]{(x-a_1)(x-a_2)......(x-a_n)}\)} where a1,a2,.....an are positive rational numbers.The limit
- In an experiment on a circuit, as shown in the figure, the voltmeter shows 8V reading. The resistance of the voltmeter is
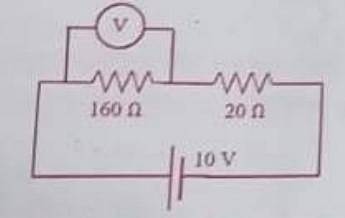
- WBJEE - 2023
- Resistance
- A rectangle ABCD has its side parallel to the line y=2x and vertices A,B,D are on y=1,x=1 and x=-1 respectively. The coordinate of C can be
- WBJEE - 2023
- Straight lines
- A missile is fired from the ground level rises x meters vertically upwards in t sec, where \(x=100t-\frac{25}{2}t^2\). the maximum height reached is
- WBJEE - 2023
- Differential equations
The equivalent weight of KIO3 in the given reaction is (M=molecular mass) :
2Cr(OH)3 + 4OH + KIO3 → 2CrO42- + 5H2O +KI- WBJEE - 2023
- Redox reactions
Concepts Used:
Vector Algebra
A vector is an object which has both magnitudes and direction. It is usually represented by an arrow which shows the direction(→) and its length shows the magnitude. The arrow which indicates the vector has an arrowhead and its opposite end is the tail. It is denoted as
The magnitude of the vector is represented as |V|. Two vectors are said to be equal if they have equal magnitudes and equal direction.
Vector Algebra Operations:
Arithmetic operations such as addition, subtraction, multiplication on vectors. However, in the case of multiplication, vectors have two terminologies, such as dot product and cross product.



