A missile is fired from the ground level rises x meters vertically upwards in t sec, where \(x=100t-\frac{25}{2}t^2\). the maximum height reached is
- 100m
- 300m
- 200m
- 125m
The Correct Option is D
Solution and Explanation
The correct answer is option (D): 125m
Given upward displacement in time t second
\(x=100t\frac{25}{2}t^2\)
Initial velocity = \(\frac{dx}{dt}=100-25t=100-25\times0=100\,m/s\)
At the maximum height velocity \(\frac{dx}{dt}=0\)
\(100-25t=0\Rightarrow t=4\)
Maximum height reached \(x=100\times4-\frac{25}{2}\times16=400-200=200m\)
Hence the maximum height reached is 200m.
The velocity of the missile, when it reaches the ground, is \((\frac{dx}{dt})_{t=8}=100-25\times 8=-100m/s.\)
Top Questions on Differential equations
- If \(\frac {dy}{dx} - \frac {(sin2x)}{(1+cos^2x)}y = \frac {sinx}{1+cos^2x }\)and \(y(0) =0\) then \(y(\frac \pi2)\) is ………..
- JEE Main - 2024
- Mathematics
- Differential equations
- Let f(x) be a continuously differentiable function on the interval (0, ∞) such that f(1) = 2 and
\(\lim\limits_{t→x}\frac{t^{10}f(x)-x^{10}f(t)}{t^9-x^9}=1\)
for each x > 0. Then, for all x > 0, f(x) is equal to- JEE Advanced - 2024
- Mathematics
- Differential equations
- If \((t+1)dx=(2x+(t+1)^3)dt\) and \(x(0)=2\), then \(x(1) \)is equal to:
- JEE Main - 2024
- Mathematics
- Differential equations
- If \(\frac{dy}{dx}\)= \(\frac{(x+y-2)}{(x-y)}\), and y(0) = 2, find y(2)
- JEE Main - 2024
- Mathematics
- Differential equations
- The solution of differential equation \(y\frac {dx}{dy}=x(log_e x-log_e y+1),\ x>0, y>0\) and passing through \((e,1)\) is
- JEE Main - 2024
- Mathematics
- Differential equations
Questions Asked in WBJEE exam
- \(\lim_{x\rightarrow \infty}\){\(x-\sqrt[n]{(x-a_1)(x-a_2)......(x-a_n)}\)} where a1,a2,.....an are positive rational numbers.The limit
- In an experiment on a circuit, as shown in the figure, the voltmeter shows 8V reading. The resistance of the voltmeter is
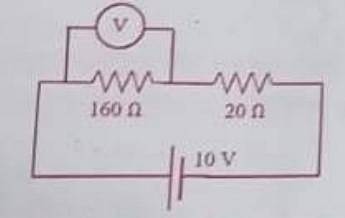
- WBJEE - 2023
- Resistance
- The value of 'a' for which the scaler triple product formed by the vectors \(\vec\alpha=\hat{i}+a\hat{j}+\hat{k}\), \(\vec{\beta}=\hat{j}+a\hat{k}\) and \(\vec{\gamma}=a\hat{i}+\hat{k}\) is maximum, is
- WBJEE - 2023
- Vector Algebra
- A rectangle ABCD has its side parallel to the line y=2x and vertices A,B,D are on y=1,x=1 and x=-1 respectively. The coordinate of C can be
- WBJEE - 2023
- Straight lines
The equivalent weight of KIO3 in the given reaction is (M=molecular mass) :
2Cr(OH)3 + 4OH + KIO3 → 2CrO42- + 5H2O +KI- WBJEE - 2023
- Redox reactions
Concepts Used:
Differential Equations
A differential equation is an equation that contains one or more functions with its derivatives. The derivatives of the function define the rate of change of a function at a point. It is mainly used in fields such as physics, engineering, biology and so on.
Orders of a Differential Equation
First Order Differential Equation
The first-order differential equation has a degree equal to 1. All the linear equations in the form of derivatives are in the first order. It has only the first derivative such as dy/dx, where x and y are the two variables and is represented as: dy/dx = f(x, y) = y’
Second-Order Differential Equation
The equation which includes second-order derivative is the second-order differential equation. It is represented as; d/dx(dy/dx) = d2y/dx2 = f”(x) = y”.
Types of Differential Equations
Differential equations can be divided into several types namely
- Ordinary Differential Equations
- Partial Differential Equations
- Linear Differential Equations
- Nonlinear differential equations
- Homogeneous Differential Equations
- Nonhomogeneous Differential Equations



