A rectangle ABCD has its side parallel to the line y=2x and vertices A,B,D are on y=1,x=1 and x=-1 respectively. The coordinate of C can be
- (3,8)
- (-3,8)
- (-3,-1)
- (3,-1)
The Correct Option is A, C
Approach Solution - 1
The coordinates of the rectangle's vertices are A(1, 1), B(1, 2), C(x, y), and D(-1, -1). The side AB lies along the line y = 2x, and the side AD is parallel to the y-axis.
The slope of AB (line segment AB) is 1−12−1=01, which is undefined. This indicates that AB is a vertical line, meaning the x-coordinates of both A and B are the same.
Therefore, C must also lie on the vertical line x = 1 to complete the rectangle. The only points that satisfy both the condition y=2x and the x-coordinate 1x=1 are (-3, -1) and (3, 6). So, the correct answer is (-3, -1) or (3, 6), which can be simplified to (-3, -1) or (3, 8) by substituting 2y=2x into the second point.
The correct answer is/are option(s):
(A): (3,8)
(C): (-3,-1)
Approach Solution -2
The slope of AB is \(\frac{1 - 1}{2 - 1} = 0\), indicating that AB is a vertical line. This means the x-coordinates of both A and B are the same.
Therefore, C must also lie on the vertical line x = 1 to complete the rectangle. The points that satisfy y = 2x and x = 1 are (-3, -1) and (3, 8).
The correct answers are:
(A): (3, 8)
(C): (-3, -1)
Top Questions on Straight lines
- If the two sides AB and AC of a triangle are along \(4x-3y-17 = 0\) and \(3x+4y-19= 0\), then the equation of the bisector of the angle between AB and AC is ?
- KEAM - 2023
- Mathematics
- Straight lines
- Ki are possible values of K for which lines \(Kx + 2y + 2 = 0\), \(2x + Ky + 3 = 0\), \(3x + 3y + K = 0\) are concurrent, then \(∑k_i\) has value.
- MHT CET - 2023
- Mathematics
- Straight lines
- Suppose the point \(P(1,1)\) is translated to \(Q\) in the direction of y = 2x. If \(PQ = 1\),then Qis
- KEAM - 2023
- Mathematics
- Straight lines
- Let the area enclosed by the $x$-axis, and the tangent and normal drawn to the curve $4 x^3-3 x y^2+6 x^2-5 x y-8 y^2+9 x+14=0$ at the point $(-2,3)$ be $A$. Then $8 A$ is equal to ______
- JEE Main - 2023
- Mathematics
- Straight lines
- Orthocentre of triangle having vertices as A (1,2), B(3,-4), C(0,6) is
- JEE Main - 2023
- Mathematics
- Straight lines
Questions Asked in WBJEE exam
- \(\lim_{x\rightarrow \infty}\){\(x-\sqrt[n]{(x-a_1)(x-a_2)......(x-a_n)}\)} where a1,a2,.....an are positive rational numbers.The limit
- In an experiment on a circuit, as shown in the figure, the voltmeter shows 8V reading. The resistance of the voltmeter is
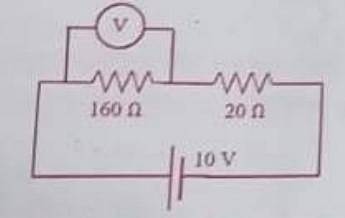
- WBJEE - 2023
- Resistance
- The value of 'a' for which the scaler triple product formed by the vectors \(\vec\alpha=\hat{i}+a\hat{j}+\hat{k}\), \(\vec{\beta}=\hat{j}+a\hat{k}\) and \(\vec{\gamma}=a\hat{i}+\hat{k}\) is maximum, is
- WBJEE - 2023
- Vector Algebra
- A missile is fired from the ground level rises x meters vertically upwards in t sec, where \(x=100t-\frac{25}{2}t^2\). the maximum height reached is
- WBJEE - 2023
- Differential equations
The equivalent weight of KIO3 in the given reaction is (M=molecular mass) :
2Cr(OH)3 + 4OH + KIO3 → 2CrO42- + 5H2O +KI- WBJEE - 2023
- Redox reactions
Concepts Used:
Straight lines
A straight line is a line having the shortest distance between two points.
A straight line can be represented as an equation in various forms, as show in the image below:

The following are the many forms of the equation of the line that are presented in straight line-
1. Slope – Point Form
Assume P0(x0, y0) is a fixed point on a non-vertical line L with m as its slope. If P (x, y) is an arbitrary point on L, then the point (x, y) lies on the line with slope m through the fixed point (x0, y0) if and only if its coordinates fulfil the equation below.
y – y0 = m (x – x0)
2. Two – Point Form
Let's look at the line. L crosses between two places. P1(x1, y1) and P2(x2, y2) are general points on L, while P (x, y) is a general point on L. As a result, the three points P1, P2, and P are collinear, and it becomes
The slope of P2P = The slope of P1P2 , i.e.
\(\frac{y-y_1}{x-x_1} = \frac{y_2-y_1}{x_2-x_1}\)
Hence, the equation becomes:
y - y1 =\( \frac{y_2-y_1}{x_2-x_1} (x-x1)\)
3. Slope-Intercept Form
Assume that a line L with slope m intersects the y-axis at a distance c from the origin, and that the distance c is referred to as the line L's y-intercept. As a result, the coordinates of the spot on the y-axis where the line intersects are (0, c). As a result, the slope of the line L is m, and it passes through a fixed point (0, c). The equation of the line L thus obtained from the slope – point form is given by
y – c =m( x - 0 )
As a result, the point (x, y) on the line with slope m and y-intercept c lies on the line, if and only if
y = m x +c



