
Collegedunia Team Content Curator
Content Curator
Moment of inertia can be defined as the quantitative measure of a body’s rotational inertia. The moment of inertia can be described as a quantity that decides the amount of torque needed for a specific angular acceleration in a rotational axis.
- It is the result of multiplying each particle's mass by the square of the distance from the axis of rotation.
- It depends on the distribution of mass around an axis of rotation.
- Depending on the axis that is chosen, the moment of inertia varies.
Read More: Radius of Gyration
Key Terms: Moment of Inertia, Angular Acceleration, Rotational Motion, Perpendicular Axis Theorem, Parallel Axis Theorem, Mass, Torque.
What is Moment of Inertia?
[Click Here for Previous Year Questions]
Moment of inertia is the “quantity represented by a body that resists angular acceleration and is the sum of the product of mass of each particle with its square of a distance from its axis of rotation.” Moment of Inertia is also known as Rotational Inertia or Angular Mass.
Moment of Inertia
- The moment of inertia can be also described as a quantity that decides the amount of torque needed for a specific angular acceleration in a rotational axis.
- The axis may be internal or external and may or may not be fixed.
- Kg m² is the SI unit of the Moment of Inertia.
Factors that Determine Moment of Inertia
Moment of inertia mainly depends on the following three factors:
- The density of the material
- Shape and size of the body
- Axis of rotation
Also Check: Radial Acceleration
Moment of Inertia Formula
[Click Here for Sample Questions]
In general form, the moment of inertia formula:
| I = m × r² |
Where,
- I = Moment of inertia.
- m = sum of the product of the mass.
- r = distance from the axis of the rotation.
M¹ L² T° is the dimensional formula of the moment of inertia.
The moment of inertia formula is given by:
| I = I = ∑mi ri² |
Calculation of Moment of Inertia
[Click Here for Previous Year Questions]
To calculate the Moment of Inertia, we use two important theorems:
- Perpendicular Axis Theorem
- Parallel Axis Theorem
Perpendicular Axis Theorem
According to the perpendicular axis theorem, the moment of inertia of a planar body about an axis perpendicular to the plane of the body is equal to the sum of the moment of inertia of the body about two perpendicular axes concurrent with the perpendicular axis and lying in the plane of the body, i.e, Iz = Ix + Iy.

Perpendicular Axis Theorem
The perpendicular axis theorem can be applied only to 2D bodies. The bodies should be flat with very less or negligible thickness.
Parallel Axis Theorem
According to the parallel axis theorem, the moment of inertia of a body about an axis parallel to the body passing through the center of mass is equal to the sum of the moment of inertia of the body about an axis passing through the center of mass and product of mass and square of the distance between the two axes, i.e, IZ’ = Iz + Mα²
Here, α = distance between two axes.

Parallel Axis Theorem
Parallel axis theorem can be applied to bodies having any shape.
- Moment of Inertia of a Uniform Rod about its Perpendicular Bisector

Uniform Rod
The Moment of inertia formula of a uniform rod about its perpendicular bisector can be expressed as:
| I = ML² / 12 |
Where,
- I = Moment of inertia
- M = Mass of the uniform rod
- L = Length of the uniform rod
Derivation of the Moment of Inertia of a Uniform Rod about its Perpendicular Bisector
Considering a uniform rod of mass M and length L and the moment of inertia should be calculated about the bisector AB.
As the rod is uniform, mass per unit length (linear mass density) remains constant.
∴ M/L = dm/dx
⇒ dm = (M/L)dx
Moment of inertia of dm,
⇒ dI = dm x²
⇒ dI = (M/L) x².dx
⇒ I = -L/2 ∫+L/2 dI
= M/L × -L/2∫+L/2 x² dx
Here,
- x = -L/2 is the left end of the rod,
- and ‘x’ changes from –L/2 to +L/2.
Now,
⇒ I = M/L × [x³/3] + L/2-L/2
⇒ I = ML²/12.
Hence,
the moment of inertia formula of a uniform rod about a perpendicular bisector is, I = ML²/12
- The Moment of Inertia of a System of Particles

Moment of Inertia of a System of Particles
The moment of inertia formula of a system of particles can be expressed as:
| I = ∑mi ri² |
Where,
- I = moment of inertia
- ri = perpendicular distance from the axis to the ith particles
- mi = mass of ith particle
- Moment of Inertia of a Rigid Body

Moment of Inertia of a Rigid Body
Moment of inertia formula of a rigid body can be expressed as:
| I = ∫r² dm |
- Moment of Inertia of Round Ring about its Axis

Moment of Inertia of Round Ring
Moment of Inertia formula of Round Ring about its Axis can be expressed as:
| I = MR² |
- Moment of Inertia of a Four-sided (Rectangular) Dish about a Line Parallel to an Edge and Passing Through the Center

Moment of Inertia of a Four-sided Dish
Moment of Inertia formula of a Four-sided (Rectangular) Dish about a Line Parallel to an Edge and Passing Through the Center can be expressed as:
| I = MI² / 12 |
If the mass of the element is parallel to the length of the plate, then the moment of inertia will be, I = Mb² / 12
- Moment of Inertia of a Uniform Circular Plate about its Axis

Moment of Inertia of a Uniform Circular Plate
Moment of Inertia formula of a Uniform Circular Plate about its Axis can be expressed as:
| I = MR² / 2 |
- Moment of Inertia of Thin Spherical Shell or Uniform Hollow Sphere

Moment of Inertia of Thin Spherical Shell
Moment of Inertia formula of Thin Spherical Shell or Uniform Hollow Sphere can be expressed as:
| I = 2MR² / 3 |
- Moment of Inertia of a Solid Sphere
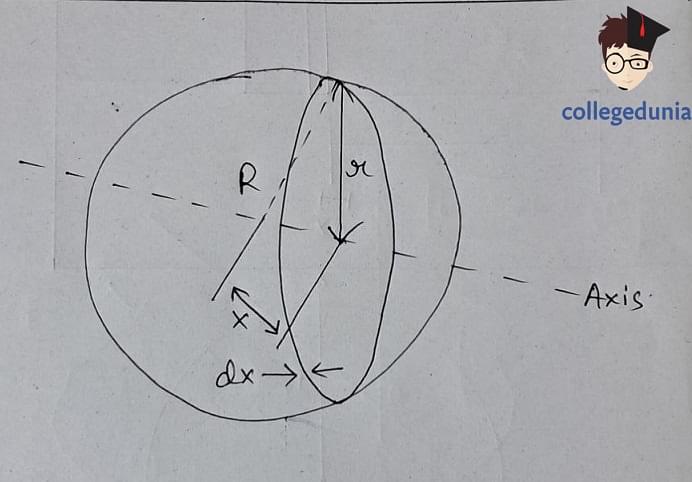
Moment of Inertia of a Solid Sphere
The moment of inertia formula of a solid sphere can be expressed as:
| I = 2MR² / 5 |
Moment of Inertia for Different Objects
[Click Here for Sample Questions]
- Moment of inertia formula of a solid cylinder about the symmetry axis will be, I = ½ MR².
- Moment of inertia formula of a hoop about the symmetry axis will be, I = MR².
- Moment of inertia formula of a solid sphere will be, I = 2/5 MR².
- Moment of inertia formula of a rod about the center will be, I = 1/12 ML².
- Moment of inertia formula of a solid cylinder about central diameter will be, I = ¼ MR² + 1/12 ML².
- Moment of inertia formula of a hoop about diameter will be, l = ½ MR².
- Moment of inertia formula of a thin spherical shell will be, I = 2/3 MR².
- Moment of inertia formula of a rod about its end will be, I = 1/3 ML².
Check More:
| Important Concept Related Topics | ||
|---|---|---|
| Rigid Bodies | Moment Formula | Law of Inertia |
| Angular Speed | Rolling Motion | Difference Between Momentum and Inertia |
| Types of lever | Linear Momentum Formula | Angular Momentum |
Things to Remember
- The moment of inertia is the quantitative measure of a body’s rotational inertia.
- Moment of Inertia is also known as Rotational Inertia or Angular Mass.
- SI unit of Moment of Inertia is Kg m².
- Moment of Inertia can be calculated by using two important theorems, Perpendicular Axis Theorem, and Parallel Axis Theorem.
- Moment of inertia formula of a solid cylinder about the symmetry axis will be, I = ½ MR².
- Moment of inertia formula of a hoop about the symmetry axis will be, I = MR².
- Moment of inertia formula of a solid sphere will be, I = 2/5 MR².
Previous Year Questions
- An L-shaped object, made of thin rods of uniform … [JEE Mains 2019]
- Consider a thin uniform square sheet made of a rigid material … [JEE Mains 2015]
- From a uniform circular disc of radius … [JEE Mains 2018]
- In a physical balance working on the principle of moments … [JEE Mains 2017]
- Let the moment of inertia of a hollow cylinder of length … [JEE Mains 2019]
- Two uniform circular discs are rotating independently … [JEE Mains 2020]
- The torque τ on a body about a given point is found to be equal … [JEE Advanced 1998]
- Two balls, having linear momenta … [JEE Advanced 2008]
- One quarter section is cut from a uniform circular disc … [JEE Advanced 2000]
- A thin wire of length L and uniform linear mass density p … [JEE Advanced 2000]
- A block of mass M has a circular cut with a frictionless … [JEE Advanced 2017]
- Consider a body, shown in figure, consisting of two identical balls … [JEE Advanced 2003]
- A particle undergoes uniform circular motion … [JEE Advanced 2003]
- The moment of inertia of a thin square plate … [JEE Advanced 1992]
- A uniform bar of mass M and Length L is bent in the form … [JKCET 2019]
- A ball of mass 0.2 kg rests on a vertical post of height 5 m … [JEE Advanced 2011]
Sample Questions
Ques. Moment of inertia mainly depends on how many factors and what are they? (1 mark)
Ans. Moment of inertia mainly depends on three factors. Those are:
- Density of the material.
- Shape and size of the body.
- Axis of rotation.
Ques. Two balls A and B are connected by a rod. The distance between ball A and ball B is 40 cm. Mass of ball A is 700 grams and the mass of ball B is 600 grams. What is the moment of inertia of the system? (2 marks)
Ans. Given,
mA = 700 grams = 0.7 kg
mB = 600 grams = 0.6 kg
rA = 0 cm = 0 m
rB = 40 cm = 0.4 m
I = mA rA² + mB rB²
I = (0.7)× (0)2 + (0.6)× (0.4)2
I = 0 + 0.096
I = 0.096 kg m²
Hence, the moment of inertia of the system is 0.096 kg m².
Ques. Two balls A and B are connected by a rod. The distance between ball A and ball B is 70 cm. Mass of ball A is 900 grams and the mass of ball B is 700 grams. What is the moment of inertia of the system? (3 marks)
Ans. Given,
mA = 900 grams = 0.9 kg
mB = 700 grams = 0.7 kg
rA = 0 cm = 0 m
rB = 70 cm = 0.7 m
I = mA rA² + mB rB²
I = (0.9)× (0)² + (0.7)× (0.7)²
I = 0 + 0.343
I = 0.343 kg m²
Hence, the moment of inertia of the system is 0.343 kg m².
Ques. What is Moment of Inertia? (2 marks)
Ans. Moment of inertia can be expressed as the quantity of a body that resists angular acceleration and is the sum of the product of mass of each particle with its square of the distance from its axis of rotation.
Ques. Consider that each ball's mass that s connected by a cord is 200 grams. The length of the cord is given as 80 cm, alongside width as 40 cm. Determine the moment of inertia of all the balls about their axis of rotation? (3 marks)
Ans. Assuming the masses of all the balls by the given equation = m1 = m2 = m3 = m4 = 200 gram = 0.2kg
Distance between ball and the axis of rotation (r1) = 40cm = 0.4 m
The same goes for ball 2, ball 3 and ball 4 = 40 cm = 0.4 m
Therefore, I = m1 r12 + m2 r22 + m3 r32 + m4 r42
⇒ I = (0.2) × (0.4)2 + (0.2) × (0.4 )2 + (0.2) × (0.4)2 + (0.2) × (0.4)2
⇒ I = 0.032 + 0.032 + 0.032 + 0.032
⇒ 0.128 kg m2
Moment of inertia is 0.128 kgm2
Ques. Define Perpendicular Axis Theorem. (2 marks)
Ans. Perpendicular axis theorem is the moment of inertia of a planar body about an axis perpendicular to the plane of the body is equal to the sum of the moment of inertia of the body about two perpendicular axes concurrent with the perpendicular axis and lying in the plane of the body, i.e, Iz = Ix + Iy.
Ques. Define Rotational Motion. (1 mark)
Ans. Rotational motion can be expressed as the rotation of bodies that remain constant throughout the whole duration of rotation over a fixed axis.
Ques. What is the moment of inertia of a Hoop about its symmetry axis? (1 mark)
Ans. Moment of inertia of a hoop about symmetry axis will be, I = MR².
Ques. What are some other names of moment of inertia? (1 mark)
Ans. Moment of Inertia is often also known as, Rotational Inertia or Angular Mass.
Also Read:







Comments