Set Theory for CAT

The most important thing about this chapter is the use of Venn diagrams, which are a key part of rational thinking. This is why this part in CAT, XLRI, FMS, CET, etc. is interesting, makes sense, and is important. Since we have to use Venn diagrams to solve most problems, the theory and ideas behind Venn diagrams are given the most attention. Formulas and mathematical theory are not very important on the CAT, but we still need to know the basics of sets and how to use them.

---

Set

[Click Here for Previous Year CAT Questions]

A set is a group of objects that is well-defined. Members or elements are the objects constituting a set. If a is an element of a set A, then we write a A (and say a belongs to A), which means 'a' is a member of 'A'. If a does not belong to A, then we write a ∉ A. By convention, sets are denoted by capital alphabets, such as A, B, C,..., X, Y, and Z, and set elements are denoted by a, b, c,...., x, y, and z, respectively.

Important Notations of Standard Sets

N: the set of natural numbers

Z⁺: the set of positive integers

Q⁺: the set of all positive rational numbers

R⁺: the set of all positive real numbers

Z : the set of integers

R : the set of real numbers

Q : the set of all rational numbers

C : the set of all complex numbers.

Methods of Representation of Sets

1. Roster Method

In this method, a set is described by enclosing a comma-separated list of all its elements within braces { } .

Ex: set of even numbers up to 20 is {2,4,6,8,10,12,14,16,18,20}

*order of the element is not important

2. Set builder Method

A set is described by listing its property in the given manner. The set P (x) is described as P = { x : P (x) holds } or { x | P (x) holds } which is read as ‘the set of all x such that P (x) holds’. The symbol ‘|’ or ‘:’ is read as ‘such that’

1. The set of perfect squares upto 100 can be written as

P = {x : x is a perfect square and 0 ≤ x ≤ 100, x ∈ N } or

P={ x: x∈N, x = n², 0 ≤ x < 100, n∈Z}

or P ={x²: x ∈ Z}

2. The set of all the odd natural numbers can be expressed as A = { x : x ∈ N , x = 2n − 1, n ∈ N }

---

Types of Sets

[Click Here for Previous Year CAT Questions]

Singleton Set : A set consisting of a single element . Ex- {0} is a singleton set.

Empty Set : A set containing no element at all is called an empty set denoted by φ. Ex- {x:x∈R, x² =−8}=φ

Finite Set : If a set has finite number of elements that can be counted or listed. Ex- set of all states in India

Cardinal Number : The number of distinct elements in a finite set is called the ‘cardinal number’ of the sete.g., n ( A) → n is the number of distinct elements in the set A.

Infinite Set : If the number of elements of a set is infinite i.e., which can’t be counted by natural numbers, is called infinite set. Ex- Set of all points on the arc of a circle

Equivalent Sets : Two finite sets A and B are equivalent if their cardinal numbers are same i.e. n ( A) = n (B ) e.g. A={a,e,i,o,u}and B={1,3,5,7,9}

Equal Sets : Two sets A and B are said to be equal, if every element of A is in B and every element of B is in A and it is denoted as A = B. Ex: A = {a,e,i,o,u} and B = {e,o,i,a,u} ⇒ A = B

Subsets : Let A and B be two sets such that every element of A is the element of B, then A is called a subset of B. Denoted by A ⊆ B

Superset : If A ⊆ B, we say that B is a superset of A and we write B ⊇ A. Read it as B is the superset of A.

Proper Subset : If A ⊆ B and AB, then A is called a proper subset of B and denoted as A ⊂ B. Ex- {5,15,25} ⊂ {5,10,15,20,25}

Properties of Subset:

1. The empty set is a subset of every set
2. Every set is a subset of itself.
3. The number of all possible subsets of a set containing n elements is 2ⁿ .
4. The number of all proper subsets of a set containing n elements is (2ⁿ − 1).
5. The set of all subsets of a given set A is called the power set of A, denoted by P (A). Thus, if A has n elements P (A) has 2ⁿ

Universal Set : A set that contains all sets in a given context is called the universal set.

Power Set : The collection or family of all the subsets of a set A is called the power set of A and is denoted by P (A).

---

Venn Diagrams

[Click Here for Previous Year CAT Questions]

Initially, the Swiss mathematician Euler explained the concept of representing sets by points on a closed curve. Later, British mathematician Venn implemented this concept. This is why the entire concept is referred to as Euler-Venn diagrams or Venn diagrams.

---

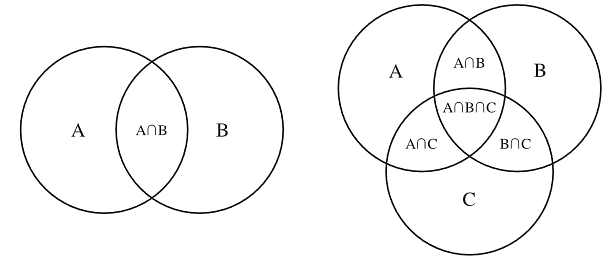
Operations On Sets

[Click Here for Previous Year CAT Questions]

Union of Sets : If A and B be two sets, then the union of A and B is the set of the all those elements which belong either to A or to B or to both A and B. Denoted as A ∪ B.

Intersection of Sets : If A and B be two sets then the intersection of A and B is the set of all those elements that belong to both A and B. Denoted by A ∩ B.

Disjoint Sets : Two sets A and B are said to be disjoint, if A∩B=φ. If A∩Bφ then A and B are said to be intersecting or overlapping sets.

Difference of Sets : The difference of set A and set B (written as A − B) is the set of all those elements of A which do not belong to B. Thus, A − B = {x : x ∈ A and x ∉ B}.

Symmetric difference of two Sets : The symmetric difference of sets A and B is the set ( A − B ) ∪ (B − A) and is denoted by A ∆ B A∆B=(A−B)∪(B−A)={x:x∉A∩B}.

Complement of a Set : If U be the universal set and a set A is such that A ⊂U then, the complement of A with respect to U is denoted by A′ or Ac.

---

Algebraic Laws of Sets

[Click Here for Previous Year CAT Questions]

1. Idempotent Laws : For any set A, we have

1.  A ∪ A = A  
2. (ii) A ∩ A = A

   2. Identity Laws : For any set A, we have

1. A ∪ φ = A
2. A ∩ U = A

3. Commutative Laws: For any two sets A and B, we have

1. A ∪ B = B ∪ A
2. A ∩ B = B ∩ A

4. Associative Laws: If A, B and C are any three sets, then

1. ( A ∪ B ) ∪ C = A ∪ (B ∪ C )
2. A ∩ ( B ∩ C) = (A ∩ B ) ∩ C

5. Distributive Laws: If A, B and C are any three sets , then

1. A ∪ (B ∩C) = (A ∪ B) ∩ (A ∪ C)

2. A ∩ (B ∪C) = (A ∩ B) ∪ (A ∩ C)

6. De-Morgan’s Laws : If A and B are any two sets, then

1. (A ∪ B)′ = A′ ∩ B′
2. (A ∩ B)′ = A′ ∪ B′

---

Important Results

[Click Here for Previous Year CAT Questions]

Operations on Numbers

1. A − B = A ∩ B′
2. B − A = B ∩ A′
3. A − B = A ⇔ A ∩ B = φ
4. (A − B) ∪ B = A ∪ B
5. (A − B) ∩ B = φ
6. A ⊆ B ⇔ B′ ⊆ A′
7. (A − B) ∪ (B − A)=(A ∪ B) − (A ∩ B)

Number of Elements in Sets

If A, B and C are finite sets, and U be the finite universal set then

1. n (A ∪ B)=n(A) + n(B) − n(A ∩ B)
2. n ( A ∪ B ) = n ( A) + n (B ) ⇔ A, B are disjoint non-void sets.
3. n(A − B) = n(A) − n(A ∩ B) i.e., n (A − B) + n (A ∩ B) = n (A)
4. n ( A ∆ B ) = Number of elements which belong to exactly one of A or B = n ( A)+ n (B ) − 2n ( A ∩ B )
5. n(A ∪ B ∪ C) = n(A) + n(B)  +n(C) − n ( A ∩ B ) − n (B ∩ C ) − n ( A ∩ C ) + n ( A ∩ B ∩ C )
6. Number of elements in exactly two of the sets A, B, C = n(A ∩ B)  +n( B ∩ C) + n(C ∩ A) − 3n(A ∩ B ∩C)
7. number of elements in exactly one of the sets A, B, C = n ( A) + n (B ) + n (C ) − 2n ( A ∩ B ) − 2n (B ∩ C)− 2n (A ∩ C)+ 3n(A ∩ B ∩C)
8. n(A′ ∪ B′) = n[(A ∩ B)′]=n(U)−n(A ∩ B)
9. n(A′ ∩ B′) = n[(A ∪ B)′ ]= n(U) − n(A ∪ B)

---

Venn Diagrams Containing Three Circles

[Click Here for Previous Year CAT Questions]

Let P, Q, R be three fruits, then

a \(\to \) number of people eating only P

b  \(\to \) number of people eating only Q

c \(\to \) number of people eating only R

x \(\to \) number of people eating P and Q both but not R

y \(\to \) number of people eating Q and R both but not P z → number of people eating P and R both but not Q k → number of people eating all the three fruits

x + k \(\to \) number of people eating P and Q both

y + k \(\to \) number of people eating Q and R both

z + k \(\to \) number of people eating P and R both

a + x + k + z \(\to \) number of people eating P

b + x + k + y \(\to \) number of people eating Q

c + y + k + z \(\to \) number of people eating R

a + x + b \(\to \) number of people eating P or Q but not R

b + y + c \(\to \) number of people eating Q or R but not P

c + z + a \(\to \) number of people eating P or R but not Q.

a + b + c \(\to \) number of people eating only one fruit

x + y + z \(\to \) number of people eating only two fruits

k \(\to \) number of people eating all of three fruits

(a + b + c) + (x + y + z) + (k ) \(\to \) number of people eating atleast one fruit

(x + y + z)+(k ) \(\to \) number of people eating atleast two fruits

(a + b + c)+(x+ y + z) + (k) \(\to \) total number of people eating fruit..

Finding the Values of Components

P + Q + R = (a + x + k + z) + (b + x + k + y) + (c + y + k + z)

P + Q+ R = (a + b + c) + 2(x + y + z) + 3k

P + Q + R = α + 2β + 3γ

where α = a + b + c,  β = x + y + z, γ = k

Again. (x + k)+(y + k)+(z + k) = (x+ y + z) + 3k = β + 3γ

(α +2β +3γ) −(β +3γ)

α +β (α +β + γ ) − (α +β) = γ

* ‘And’ means intersection, ‘or’ means union