Question:
For one mole of a van der Waals' gas when $b = 0$ and $T = 300\, K$. the $pV\, vs \,1/V$ plot is shown below. The value of the van der Waals' constant a (atm $L\, mol^{-2}$)
For one mole of a van der Waals' gas when $b = 0$ and $T = 300\, K$. the $pV\, vs \,1/V$ plot is shown below. The value of the van der Waals' constant a (atm $L\, mol^{-2}$)
Updated On: Jun 14, 2022
- 1
- 4.5
- 1.5
- 3
Hide Solution
Verified By Collegedunia
The Correct Option is C
Solution and Explanation
The van der Waals equation of state is
$\, \, \, \, \, \, \, \, \, \, \, \, \, \Bigg(p+\frac{n^ a}{V^2}\Bigg)(V-nb)=nRT$
For one mole and when b = 0, the above equation condenses to
$\, \, \, \, \, \, \, \, \, \, \, \, \, \Bigg(p+\frac{n^ a}{V^2}\Bigg)V=RT$
$\Rightarrow \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, pV=RT-\frac{a}{V}\, \, \, \, \, \, \, \, \, ...(i)$
E (i) is a straight equation between pV and$\frac{1}{V}$ whose slope is -
- a'. Equating with slope of the straight line given in the graph.
$\, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, -a=\frac{20.1-21.6}{3-2}=-1.5$
$\Rightarrow \, \, \, \, \, \, \, \, \, \, \, a=1.5$
$\, \, \, \, \, \, \, \, \, \, \, \, \, \Bigg(p+\frac{n^ a}{V^2}\Bigg)(V-nb)=nRT$
For one mole and when b = 0, the above equation condenses to
$\, \, \, \, \, \, \, \, \, \, \, \, \, \Bigg(p+\frac{n^ a}{V^2}\Bigg)V=RT$
$\Rightarrow \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, pV=RT-\frac{a}{V}\, \, \, \, \, \, \, \, \, ...(i)$
E (i) is a straight equation between pV and$\frac{1}{V}$ whose slope is -
- a'. Equating with slope of the straight line given in the graph.
$\, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, -a=\frac{20.1-21.6}{3-2}=-1.5$
$\Rightarrow \, \, \, \, \, \, \, \, \, \, \, a=1.5$
Was this answer helpful?
0
0
Top Questions on States of matter
- A closed vessel contains 10 g of an ideal gas X at 300 K, which exerts 2 atm pressure. At the same temperature, 80 g of another ideal gas Y is added to it and the pressure becomes 6 atm. The ratio of root mean square velocities of X and Y at 300 K is
- JEE Advanced - 2024
- Chemistry
- States of matter
- Number of molecules and moles in 2.8375 litre of O2 at STP.
- JEE Main - 2023
- Chemistry
- States of matter
- Which of the following is a physical change?
- NATA - 2023
- Chemistry
- States of matter
NaOH is deliquescent
- BITSAT - 2023
- Chemistry
- States of matter
Intermolecular forces are forces of attraction and repulsion between interacting paiticles that will include :
A. dipole - dipole forces.B. dipole - induced dipole forces.C. hydrogen bonding.D. covalent bonding.E. dispersion forces.Choose the most appropriate answer from the options given below :- NEET (UG) - 2023
- Chemistry
- States of matter
View More Questions
Questions Asked in JEE Advanced exam
- A region in the form of an equilateral triangle (in x-y plane) of height L has a uniform magnetic field 𝐵⃗ pointing in the +z-direction. A conducting loop PQR, in the form of an equilateral triangle of the same height 𝐿, is placed in the x-y plane with its vertex P at x = 0 in the orientation shown in the figure. At 𝑡 = 0, the loop starts entering the region of the magnetic field with a uniform velocity 𝑣 along the +x-direction. The plane of the loop and its orientation remain unchanged throughout its motion.
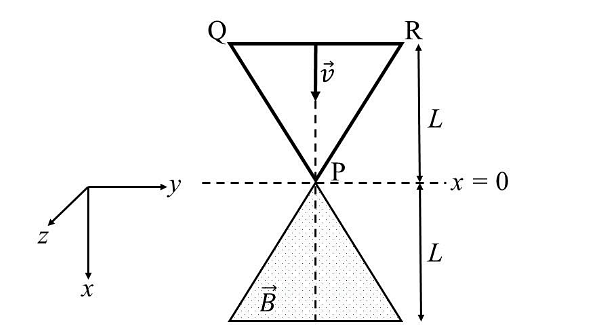
Which of the following graph best depicts the variation of the induced emf (E) in the loop as a function of the distance (𝑥) starting from 𝑥 = 0? - Two beads, each with charge q and mass m, are on a horizontal, frictionless, non-conducting, circular hoop of radius R. One of the beads is glued to the hoop at some point, while the other one performs small oscillations about its equilibrium position along the hoop. The square of the angular frequency of the small oscillations is given by [ \(\epsilon_0 \)is the permittivity of free space.]
- JEE Advanced - 2024
- Moving charges and magnetism
- A group of 9 students, s1, s2,…., s9, is to be divided to form three teams X, Y and Z of sizes 2, 3, and 4, respectively. Suppose that s1 cannot be selected for the team X and s2 cannot be selected for the team Y. Then the number of ways to form such teams, is _______.
- JEE Advanced - 2024
- Combinations
- Let \(\vec{p}=2\hat{i}+\hat{j}+3\hat{k}\) and \(\vec{q}=\hat{i}-\hat{j}+\hat{k}\). If for some real numbers α, β and γ we have
\(15\hat{i}+10\hat{j}+6\hat{k}=α(2\vec{p}+\vec{q})+β(\vec{p}-2\vec{q})+γ(\vec{p}\times\vec{q})\),
then the value of γ is ________.- JEE Advanced - 2024
- Vector Algebra
- Let X be a random variable, and let P(X = x) denote the probability that X takes the value x. Suppose that the points (x, P(X = x)), x = 0,1,2,3,4, lie on a fixed straight line in the xy -plane, and P(X = x) = 0 for all x ∈ R - {0,1,2,3,4}. If the mean of X is \(\frac{5}{2}\) , and the variance of X is α, then the value of 24α is ______.
- JEE Advanced - 2024
- Probability
View More Questions
Concepts Used:
States of Matter
The matter is made up of very tiny particles and these particles are so small that we cannot see them with naked eyes.
There are three States of Matter:
The three states of matter are as follows:
Solid State:
- The solid-state is one of the fundamental states of matter.
- Solids differ from liquids and gases by the characteristic of rigidity.
- The molecules of solids are tightly packed because of strong intermolecular forces; they only oscillate about their mean positions.
Liquid State:
- The molecules in a liquid are closely packed due to weak intermolecular forces.
- These forces are weaker than solids but stronger than that of gases.
- There is much space in between the molecules of liquids which makes their flowing ability easy.
Gaseous State:
- In this state of matter, distances between the molecules are large (intermolecular distance is in the range of 10-7-10-5 cm.
- The intermolecular forces experienced between them are negligible.
- Thus, translatory, rotatory and vibratory motions are observed prominently in gases.



