For $0 \leq p \leq 1$ and for any positive $a, b$ let $I(p) = (a + b)^p, J(p) = a^p + b^p$, then
- $I (p) > J (p)$
- $I (p) \leq J (p)$
- $I(p) < J(p)$ in $[0, \frac{P}{2} ]$ & $I(p) > J(p)$ in $[\frac{P}{2} , \infty )$
- $I(p) < J(p)$ in $[\frac{P}{2}, \infty )$ & $J(p) > I(p)$ in $[0, \frac{P}{2}]$
The Correct Option is B
Solution and Explanation
Given that;
For any positive a,b; let \(I(p)=(a+b)^b. J(p)=a^b+b^b\)
For 0≤p≤1
Then let us take a=3 , b=4
then p=0.5
\(i(p)=5; J(p)=7\)
\(\therefore J(p)>I(p)\)
Now a= ⅓, b= ¼
when p=1
\(I(p)= \frac{7}{12}; J(p)=\frac{7}{12}\)
\(\therefore I(p)=J(p)\)
\(I(p)\)≤\(J(p)\)
Top Questions on Increasing and Decreasing Functions
- If $f(x) = x^2 + bx + 1$ is increasing in the interval $[1, 2]$, then the least value of $b$ is:
- CUET (UG) - 2024
- Mathematics
- Increasing and Decreasing Functions
- Given: \(5f (x) 4f(\frac 1x) = x^2 - 4 \) & \(y = 9f(x) × x^2\) If y is strictly increasing, then find interval of \(x\).
- JEE Main - 2024
- Mathematics
- Increasing and Decreasing Functions
- In which interval the function \(f(x) = \frac {x}{(x^2-6x-16)}\) is increasing?
- JEE Main - 2024
- Mathematics
- Increasing and Decreasing Functions
- Let \(f:→R→(0,∞)\) be increasing function such that \(Lt_{x→∞}\frac {f(7x)}{f(x)}=1\), then \(Lt_{x→∞}[\frac {f(5x)}{f(x)}-1]\) is equal to
- JEE Main - 2024
- Mathematics
- Increasing and Decreasing Functions
- Let $\alpha \in(0,1)$ and $\beta=\log _e(1-\alpha)$ Let $P_n(x)=x+\frac{x^2}{2}+\frac{x^3}{3}+\ldots+\frac{x^n}{n}, x \in(0,1)$ Then the integral $\int\limits_0^\alpha \frac{t^{50}}{1-t} d t$ is equal to
- JEE Main - 2023
- Mathematics
- Increasing and Decreasing Functions
Questions Asked in WBJEE exam
- \(\lim_{x\rightarrow \infty}\){\(x-\sqrt[n]{(x-a_1)(x-a_2)......(x-a_n)}\)} where a1,a2,.....an are positive rational numbers.The limit
- A particle of mass m is projected at velocity at a velocity u, making an angle θ with the horizontal(x-axis). If the angle of projection θ is varied keeping all other parameters same, then magnitude of angular momentum(L) at its maximum height about the point of projection varies with θ as,
- WBJEE - 2023
- System of Particles & Rotational Motion
- If \(\int \frac{dx}{(x+1)(x-2)(x-3)}=\frac{1}{k}log_e\left \{ \frac{|x-3|^3|x+1|}{(x-2)^4}\right \}+c\), then the value of k is
- WBJEE - 2023
- Integrals of Some Particular Functions
- A rectangle ABCD has its side parallel to the line y=2x and vertices A,B,D are on y=1,x=1 and x=-1 respectively. The coordinate of C can be
- WBJEE - 2023
- Straight lines
- In an experiment on a circuit, as shown in the figure, the voltmeter shows 8V reading. The resistance of the voltmeter is
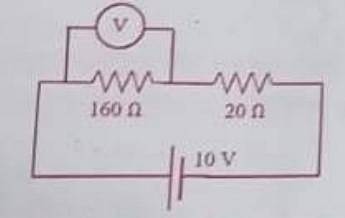
- WBJEE - 2023
- Resistance
Concepts Used:
Increasing and Decreasing Functions
Increasing Function:
On an interval I, a function f(x) is said to be increasing, if for any two numbers x and y in I such that x < y,
⇒ f(x) ≤ f(y)
Decreasing Function:
On an interval I, a function f(x) is said to be decreasing, if for any two numbers x and y in I such that x < y,
⇒ f(x) ≥ f(y)
Strictly Increasing Function:
On an interval I, a function f(x) is said to be strictly increasing, if for any two numbers x and y in I such that x < y,
⇒ f(x) < f(y)
Strictly Decreasing Function:
On an interval I, a function f(x) is said to be strictly decreasing, if for any two numbers x and y in I such that x < y,
⇒ f(x) > f(y)
Graphical Representation of Increasing and Decreasing Functions




