
Collegedunia Team Content Curator
Content Curator
Resultant Vector Formula is used to obtain the resultant value of two or more vectors based on their directions with respect to each other. When two or more forces operate on a body, the resultant force or net force is the sum of all the forces that generate the effect. To get the resultant value of two or more vectors, we apply the resultant vector formula. The resulting vector formula can be used in physics, engineering and mathematics. The three resultant vector formulas are:
R = A + B
R = A - B
R2 = A2 + B2 + 2ABCos Θ
The interaction of several force vectors on a body is an example of the resultant vector, and the resulting vector is obtained using this formula.
| Table of Content |
What is Vector Quantity?
[Click Here for Previous Year Questions]Vector Quantity is a physical quantity that is specified not only by its magnitude but also by its direction. A vector quantity whose magnitude is equal to one and has direction is called a unit vector.
Examples of vector quantity are-
- Displacement
- Linear momentum
- Momentum
- Acceleration
- Force
- Electric field
- Angular velocity
- Polarization
Also Check:
| Read More about Vectors | ||
|---|---|---|
| Resolution of Vectors | Displacement vector | velocity vectors |
| Trajectory formula | Horizontal Motion | Projectile Motion Formula |
What is the Resultant Vector Formula?
[Click Here for Previous Year Questions]The resultant vector formula may be divided into three types on the basis of the orientation of the vectors. These formulae are applicable to vectors pointing in the same direction, vectors pointing in opposing directions, and vectors that are inclined to each other.
Resultant Vector Formula 1
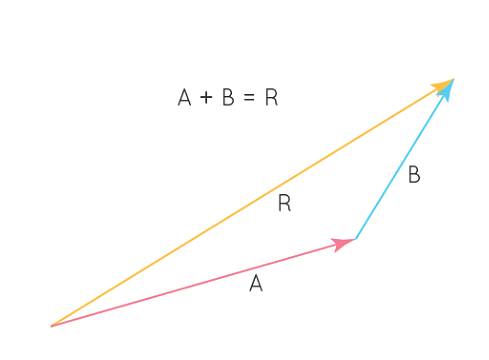
If the vectors are aligned in the same direction then the resulting vector can be obtained by simply adding them.
Let, A and B are the same-direction vectors, while R is the resulting vector. So,
R = A + B
Resultant Vector Formula 2
The vectors that are aligned in opposite directions are subtracted from each other to produce the resulting vector. Let, vector B is in the opposite direction of vector A. So, the resultant vector R is
R = A - B
Resultant Vector Formula 3
If the given vectors are inclined to each other then the resultant vector can be obtained by using the formula below. Here, R is the resultant vector, and A and B are inclined at an angle Θ to each other.
R2 = A2 + B2 + 2ABCos Θ
Resultant Vector Formula 3
Also Check:
| Learn more topics from Motion in Plane Chapter | ||
|---|---|---|
| Displacement | Angular Momentum | Acceleration |
| Angular Speed | Polarization | Electric Field |
| Centripetal Acceleration | Uniform Circular Motion | Tangential Acceleration Formula |
| Relation between torque and speed | Equations of Motion | Distance Time Graph |
Things to Remember
- A vector quantity is a physical quantity that has both direction and magnitude.
- When two or more forces act on a body, the resulting force, also known as the net force, is equal to the total of all the forces that produce the effect.
- The resultant vector of the vectors that are aligned in the same direction can be evaluated by simply adding the two vectors. R = A + B
- Vectors that are aligned in opposite directions are subtracted from each other to get the final resultant vector. R = A - B
- Compute vectors inclined to each other using the formula below to get the resultant vector. In this case, R is the resulting vector, and A and B are at an angle to each other. R2 = A2 + B2 + 2ABCosΘ
Sample Questions
Ques: On a straight road, an automobile starts from point A and travels west for 20 seconds, arriving at position B, which is 200 metres distant. After 30 seconds, the automobile returns to the east, arriving at location C, which is 800 metres away from B. What is the car's displacement from point A? (2 Marks)
Ans: The automobile leaves point A and travels west for 20 seconds, arriving at location B, which is 200 metres distant. This corresponds to a -200 m displacement.
After 30 seconds, the automobile returns to the east, arriving at location C, which is 800 metres away from B. This corresponds to a displacement of +800 metres.
As a result, the car's overall displacement is -200 +800 = + 600 m.
Ques: Find the resultant of the vectors 4i + 3j -5k and 8i + 6j - 10k. (2 Marks)
Ans: Given two vectors are:
A = 4i + 3j - 5k and B = 8i + 6j - 10k
Because the direction ratios of the two vectors are equal, the two vectors are pointing in the same direction.
R = A + B
= (4i+3j-5k) + (8i+6j-10k)
= 12i+9j -15k
Ques: Two vectors, F1 = 20 N and F2 = 30 N, have directions as shown in the figure below. Determine the resultant of components of vectors in the x-axis and y-axis. (3 Marks)

Ans: Given that-
F1 = 20 Newton
Angle between F1 and x axis = 30°
F2 = 30 Newton
Angle between F2 and x axis =30°
F1x = F1 cos 30°= (20)(0.5√3) = 10√3 Newton (plus sign because it points to the x-axis)
F1y = F1 sin 30° = (20)(0.5) = 10 Newton ( plus sign because it points to the +y axis)
F2x = F2 cos 30° = (30)(0.5√3) = -15√3 Newton (plus sign because it points to the -x axis)
F2y = F2 sin 30° = (30)(0.5) = 15 Newton (plus sign because it points to the +y axis)
The resultant of the x component is:
Fx = F1x+F2x
= 10√3 N – 15√3 N
= -5√3 N
The resultant of the y component is:
Fy = F1y + F2y
= 10N + 15N
= 25 N
Ques: Determine the resultant of two vectors with magnitudes of 5 and 6 units and an angle of 60 degrees between them. (3 Marks)
Ans: The two vectors are
A = 5 units,
B = 6 units
the angle Θ = 60°.
R2 = A2 + B2 + 2ABCos Θ
= 52 + 62 + 2 × 5 × 6 × Cos60°
= 25 + 36 + 60*1/2
= 61 + 30
R2 = 91
\(R = \sqrt{91} \)
Ques: Someone riding a motorbike 6 kilometres north and then 8 kilometres east from their residence. Determine the person's ultimate position based on their beginning position. (3 Marks)

Ans: Given that:
A = 6
B = 8
The angle Θ = 90°.
R2 = 62 + 82 + 2 x 6 x 8 x Cos 90°
\(R = \sqrt{36 + 64}\)
\(R = \sqrt{100}\)
R = 10 km , northeast
Ques: A car travels from A to B along 30 km north, then 60 km east, then 110 km south. Calculate the displacement of the car from A to D. (3 Marks)
Ans: AA’ = 60 km
A’D = 110 km – 30 km
= 80 km
R2 = (AA’)2 + (A’D)2
R2 = (60)2 + (80)2
\(R = \sqrt {3600 + 6400}\)
\(R = \sqrt{10000}\)
R = 100

Ques: Sabrina took a 75-meter trek east. She then walked 25 metres while turning 30 degrees to the left. Determine Sabrina's displacement vector's magnitude. (3 Marks)
Ans: Given that-
A = 75 meter
B = 25 meter
The angle Θ = 30°.
R2 = A2 + B2 + 2ABCos 30°
R2 = 752 + 252 + 2 (75)(25) \(\frac{\sqrt{3}}{2}\)
\(R = \sqrt{5625 +625 +3247.5}\)
R = 97.46 meter
Ques: Find the angle alpha and the magnitude of a resultant vector. (5 Marks)

Ans:


Do Check Out:






Comments