N capacitors,each with 1μF capacitance,are connected in parallel to store a charge of 1C. The potential across each capacitor is 100V. If these N capacitors are now connected in series,the equivalent capacitance in the circuit will be:
- 10-4F
- 10-6F
- 10-10F
- 5x10-8F
- 10-2F
The Correct Option is C
Approach Solution - 1
The correct answer is (C): 10-10F
Approach Solution -2
Given,
- Capacitors are connected in parallel with capacitance \(C = 1 \mu F = 1 \times 10^{-6} F\).
- Total charge stored, Q = 1C.
- Potential across each capacitor, V = 100V.
1. Finding the number of capacitors N in parallel:
We use the formula \(Q = C \cdot V\), where Q is the total charge, C is the capacitance, and V is the voltage.
\(\begin{aligned} Q & = C \cdot V \\ 1 & = N \cdot (1 \times 10^{-6}) \cdot 100 \\ N & = \frac{1}{1 \times 10^{-6} \cdot 100} \\ & = \frac{1}{10^{-4}} \\ & = 10^4 \end{aligned}\)
So, there are \(N = 10^4\) capacitors connected in parallel.
2. Finding the equivalent capacitance when capacitors are connected in series:
When capacitors are connected in series, the equivalent capacitance \(C_{\text{eq}}\) is given by the reciprocal of the sum of the reciprocals of individual capacitances.
\(\frac{1}{C_{\text{eq}}} = \frac{1}{C_1} + \frac{1}{C_2} + \cdots + \frac{1}{C_N}\)
Substituting the values, since each capacitor has the same capacitance \(( C_1 = C_2 = \cdots = C_N = 1 \mu F )\):
\(\frac{1}{C_{\text{eq}}} = \frac{1}{1 \times 10^{-6}} + \frac{1}{1 \times 10^{-6}} + \cdots + \frac{1}{1 \times 10^{-6}} \quad (N \text{ times})\)
\(\frac{1}{C_{\text{eq}}} = N \times \frac{1}{1 \times 10^{-6}}\)
\(C_{\text{eq}} = \frac{1 \times 10^{-6}}{N}\)
\(C_{\text{eq}} = \frac{1 \times 10^{-6}}{10^4}\)
\(C_{\text{eq}} = 1 \times 10^{-10} F\)
So, the correct option is (C): \(10^{-10} F\)
Top Questions on Capacitors and Capacitance
- A 10 µF capacitor is connected to a 210 V, 50 Hz source as shown in figure. The peak current in the circuit is nearly (π = 3.14) :
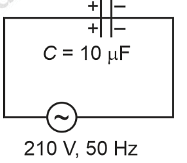 :
:- NEET (UG) - 2024
- Physics
- Capacitors and Capacitance
- In the following circuit, the equivalent capacitance between terminal A and terminal B is :
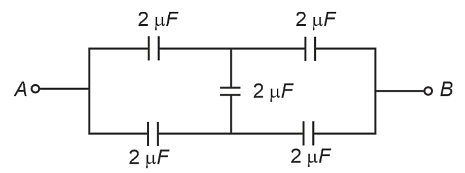
- NEET (UG) - 2024
- Physics
- Capacitors and Capacitance
- A parallel plate capacitor is charged by connecting it to a battery through a resistor. If I is the current in the circuit, then in the gap between the plates :
- NEET (UG) - 2024
- Physics
- Capacitors and Capacitance
- A capacitor having capacitance of 100uF is charged with a potential difference of 12 V is connected to an inductor of inductance 10 mH. Find the maximum current through the inductor.
- JEE Main - 2024
- Physics
- Capacitors and Capacitance
- A capacitor of capacitance 150.0 µF is connected to an alternating source of emf given by E = 36 sin(120πt) V. The maximum value of current in the circuit is approximately equal to
- JEE Main - 2023
- Physics
- Capacitors and Capacitance
Questions Asked in KEAM exam
- If the two sides AB and AC of a triangle are along \(4x-3y-17 = 0\) and \(3x+4y-19= 0\), then the equation of the bisector of the angle between AB and AC is ?
- KEAM - 2023
- Straight lines
- An average frictional force of 80N is required to stop an object at a distance of 25m. If the initial speed of the object is 20m/s,the mass of the object is:
- KEAM - 2023
- work, energy and power
- A biased die is rolled such that the probability of getting k dots,1≤k≤6, on the upper face of the die is proportional to k. Then the probability that five dots appear on the upper face of the die is
- KEAM - 2023
- Probability
- A planet has an escape speed of 10km/s,The radius of the planet is 10,000km. The acceleration due to gravity of the planet at its surface is:
- KEAM - 2023
- Gravitation
- \(∫xlog(1+x^2)dx=\)?
- KEAM - 2023
- Integration by Parts
Concepts Used:
Combination of Capacitors
The total capacitance of this equivalent single capacitor depends both on the individual capacitors and how they are connected. There are two simple and common types of connections, called series and parallel, for which we can easily calculate the total capacitance.
Read Also: Combination of Capacitors
Series capacitors
When one terminal of a capacitor is connected to the terminal of another capacitors , called series combination of capacitors.
Capacitors in Parallel
Capacitors can be connected in two types which are in series and in parallel. If capacitors are connected one after the other in the form of a chain then it is in series. In series, the capacitance is less.
When the capacitors are connected between two common points they are called to be connected in parallel.
When the plates are connected in parallel the size of the plates gets doubled, because of that the capacitance is doubled. So in a parallel combination of capacitors, we get more capacitance.
Read More: Types of Capacitors



