In an oil drop experiment, 'n' numbers of electrons are stripped from an oil drop to make it positively charged. A vertical electric field of magnitude 4.9x1014 N/C is applied to balance the force due to gravity on the oil drop. If the mass of oil drop is 80 μg,the value of 'n' will be:(Take g =9.8 m/s2 and charge of an electron = 1.6 x 10-19 C)
- 1
- 10
- 100
- 1000
- 10000
The Correct Option is B
Approach Solution - 1
The correct answer is (B):10
Approach Solution -2
Let's Convert the mass of oil drop to kilograms.
Given: Mass of oil drop = 80 μg = 80 × 10^-6 kg
Calculate force due to gravity.
Given: Gravity (g) = 9.8 m/s²
Formula: Force gravity = mass of oil drop \(\times\) gravity
Force gravity = \(80 \times 10^{-6} \, \text{kg} \times 9.8 \, \text{m/s}^2\)
\(=\gt 7.84 \times 10^{-4} \, \text{N}\)
Balance forces using an electric field.
Given: Electric field strength \(E = 4.9 \times 10^{14}\ N/C\)
Solve for total charge (q).
Formula: \(\text{q} = \frac{\text{force\_gravity}}{\text{E}}\)
\(\text{q} = \frac{7.84 \times 10^{-4} \, \text{N}}{4.9 \times 10^{14} \, \text{N/C}}\)
\(\text{q} = 1.6 \times 10^{-18} \, \text{C}\)
the number of missing electrons (n).
Given: Charge of a single electron = \(1.6 \times 10^{-19}\ C\)
Formula: \(\text{n} = \frac{\text{q}}{\text{charge\_of\_electron}}\)
\(\text{n} = \frac{|1.6 \times 10^{-18} \, \text{C}|}{1.6 \times 10^{-19} \, \text{C}}\)
\(\text{n} = 10\)
So, the correct option is (B): 10
Top Questions on Electric charges and fields
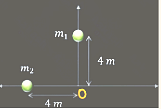
- Two particles each of mass \(2\) kg are places as shown in \(x→ y\) plane. If the distance of centre of mass from origin is \(\frac{4\sqrt 2}{x}\) find \(x\) :
- JEE Main - 2024
- Physics
- Electric charges and fields
- A uniform electric field of $10 N / C$ is created between two parallel charged plates (as shown in figure) An electron enters the field symmetrically between the plates with a kinetic energy $05 eV$ The length of each plate is $10 cm$ The angle $(\theta)$ of deviation of the path of electron as it comes out of the field is ___ (in degree)

- JEE Main - 2023
- Physics
- Electric charges and fields
- Electric field in a certain region is given by $\overrightarrow{ E }=\left(\frac{ A }{x^2} \hat{i}+\frac{ B }{y^3} \hat{j}\right)$ The $SI$ unit of $A$ and $B$ are :
- JEE Main - 2023
- Physics
- Electric charges and fields
Given below are two statements : One is labelled as Assertion $A$ and the other is labelled as Reason R
Assertion A : Two metallic spheres are charged to the same potential One of them is hollow and another is solid, and both have the same radii Solid sphere will have lower charge than the hollow one
Reason R : Capacitance of metallic spheres depend on the radii of spheres
In the light of the above statements, choose the correct answer from the options given belows- JEE Main - 2023
- Physics
- Electric charges and fields
- A 10 μC charge is divided into two equal parts and kept at 1 cm distance. Find repulsion between charges?
- JEE Main - 2023
- Physics
- Electric charges and fields
Questions Asked in KEAM exam
- If the two sides AB and AC of a triangle are along \(4x-3y-17 = 0\) and \(3x+4y-19= 0\), then the equation of the bisector of the angle between AB and AC is ?
- KEAM - 2023
- Straight lines
- An average frictional force of 80N is required to stop an object at a distance of 25m. If the initial speed of the object is 20m/s,the mass of the object is:
- KEAM - 2023
- work, energy and power
- A biased die is rolled such that the probability of getting k dots,1≤k≤6, on the upper face of the die is proportional to k. Then the probability that five dots appear on the upper face of the die is
- KEAM - 2023
- Probability
- A planet has an escape speed of 10km/s,The radius of the planet is 10,000km. The acceleration due to gravity of the planet at its surface is:
- KEAM - 2023
- Gravitation
- \(∫xlog(1+x^2)dx=\)?
- KEAM - 2023
- Integration by Parts
Concepts Used:
Electric Field
Electric Field is the electric force experienced by a unit charge.
The electric force is calculated using the coulomb's law, whose formula is:
\(F=k\dfrac{|q_{1}q_{2}|}{r^{2}}\)
While substituting q2 as 1, electric field becomes:
\(E=k\dfrac{|q_{1}|}{r^{2}}\)
SI unit of Electric Field is V/m (Volt per meter).



