Select Goal &
City
Select Goal
Explore
Question:
A 1 kg ball moving at 12 ms-1 collides with a 2 kg ball moving in opposite direction at 24 ms-1. If the coefficient of restitution is \(\frac{2}{3}\), then the velocities after the collision are
A 1 kg ball moving at 12 ms-1 collides with a 2 kg ball moving in opposite direction at 24 ms-1. If the coefficient of restitution is \(\frac{2}{3}\), then the velocities after the collision are
Updated On: Apr 17, 2024
- -4 ms-1, - 28 ms-1
- -28 ms-1, -4 ms-1
- 4 ms-1, 28 ms-1
- 28 ms-1, 4 ms-1
Hide Solution
Verified By Collegedunia
The Correct Option is B
Solution and Explanation
The correct answer is (B) : -28 ms-1, -4 ms-1.
Was this answer helpful?
0
0
Top Questions on Elastic and inelastic collisions
- Two particles, 1 and 2, each of mass 𝑚, are connected by a massless spring, and are on a horizontal frictionless plane, as shown in the figure. Initially, the two particles, with their center of mass at \(𝑥_0\), are oscillating with amplitude 𝑎 and angular frequency 𝜔. Thus, their positions at time 𝑡 are given by \(x_1 (t) = (x_0 + d) + \alpha \ sin \omega t\) and \(x_2t = (x_0 -d) − \alpha sin \ wt,\) respectively, where \(𝑑 > 2𝑎.\) Particle 3 of mass 𝑚 moves towards this system with speed 𝑢0 = 𝑎𝜔/2, and undergoes instantaneous elastic collision with particle 2, at time \(𝑡_0\). Finally, particles 1 and 2 acquire a center of mass speed \(𝑣_{cm}\) and oscillate with amplitude 𝑏 and the same angular frequency 𝜔.
- JEE Advanced - 2024
- Physics
- Elastic and inelastic collisions
- Choose the option showing the correct relation between Poisson’s ratio (σ), Bulk modulus (B) and modulus of rigidity (G).
- JEE Main - 2023
- Physics
- Elastic and inelastic collisions
- A uniform heavy rod of mass \(20\) kg, cross sectional area \(0.4\) \(m^2\) and length \(20\) \(m\) is hanging from a fixed support. Neglecting the lateral contraction, the elongation in the rod due to its own weight is \(x × 10^{–9}\) \(m\). The value of \(x\) is _____(Given Young’s modulus \(Y = 2 × 10^{11} Nm^{–2}\)and g = \(10\; ms^{–2})\)
- JEE Main - 2022
- Physics
- Elastic and inelastic collisions
- Which one of the following is the correct statement?
- KEAM - 2022
- Physics
- Elastic and inelastic collisions
- A ball hits the floor and rebounds after an inelastic collision. In this case
- KCET - 2021
- Physics
- Elastic and inelastic collisions
View More Questions
Questions Asked in KCET exam
- A cubical Gaussian surface has side of length a = 10 cm. Electric field lines are parallel to x-axis as shown. The magnitudes of electric fields through surfaces ABCD and EFGH are 6kNC-1 and 9kNC-1 respectively. Then the total charge enclosed by the cube is
[Take ε0 = 9 × 10-12 Fm-1]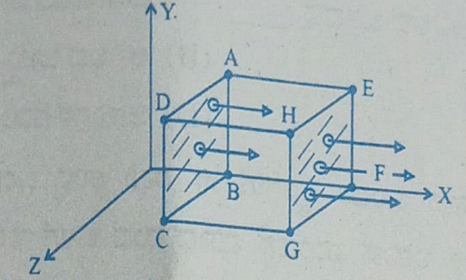
- KCET - 2023
- Gauss Law
- A sample of water is found to contain 5.85% \((\frac{w}{w})\) of AB (molecular mass 58.5) and 9.50% \((\frac{w}{w})\) XY2 (molecular mass 95). Assuming 80% ionisation of AB and 60% ionisation of XY2 , the freezing point of water sample is
[Given : Kf for water 1.86 K kg mol-1 , Freezing point of pure water is 273 K and A, B and Y are monovalent ions]- KCET - 2023
- Colligative Properties
- \(aMnO^{-}_4+bS_2O_{3}^-+H_2O\rightarrow xMnO_2+ySO_{4}^-+zOH^-\)
a and y respectively are- KCET - 2023
- Redox reactions
- \(\int\sqrt{\cosec x-\sin x}\ dx=\)
- KCET - 2023
- Definite Integral
- A metallic rod of length 1 m held along east-west direction is allowed to fall down freely. Given horizontal component of earth’s magnetic field BH = 3 × 10-5 T. The emf induced in the rod at an instant t = 2s after it is released is ( Take g = 10 ms-2 )
- KCET - 2023
- Faradays laws of induction
View More Questions
SUBSCRIBE TO OUR NEWS LETTER
COLLEGE NOTIFICATIONSEXAM NOTIFICATIONSNEWS UPDATES
Download the Collegedunia app on 
© 2024 Collegedunia Web Pvt. Ltd. All Rights Reserved