The sum of first 9 terms of the series $ \frac{1^3}{1} + \frac{1^3+2^3}{1+3} + \frac{1^3+2^3+3^3}{1+3+5} +...$ is
- 71
- 96
- 142
- 192
The Correct Option is B
Solution and Explanation
Top Questions on Arithmetic Progression
- If the 20th term from the end of the progression 20,19\({\frac{1}{4}}\) ,18\({\frac{1}{2}}\) ,17\({\frac{3}{4}}\) ,……, -129\({\frac{1}{4}}\) is______?
- JEE Main - 2024
- Mathematics
- Arithmetic Progression
- In an increasing arithmetic progression \(a_1, a_2,..., a_n\) if \(a_6 = 2\) and product of \(a_1\), \(a_5\) and \(a_4\) is greatest, then the value of d is equal to
- JEE Main - 2024
- Mathematics
- Arithmetic Progression
- Let m and n be the coefficient of \(7^{th}\) and \(13^{th}\) term in expansion of \(\bigg(\frac{1}{3x^{\frac{1}{3}}} +\frac{1}{2x^{\frac{2}{5}}}\bigg)^{18}\), then \(\bigg(\frac{m}{n}\bigg)^{\frac{1}{3}}\) is:
- JEE Main - 2024
- Mathematics
- Arithmetic Progression
- If ln a, ln b, ln c are in AP and ln a – ln 2b, ln 2b – ln 3c, ln 3c – ln a are in AP then a : b : c is
- JEE Main - 2024
- Mathematics
- Arithmetic Progression
- If 2nd, 8th, 44th terms of A.P. are 1st, 2nd and 3rd terms respectively of G.P. and first term of A.P. is 1 then the sum of first 20 terms of A.P. is
- JEE Main - 2024
- Mathematics
- Arithmetic Progression
Questions Asked in JEE Advanced exam
- A region in the form of an equilateral triangle (in x-y plane) of height L has a uniform magnetic field 𝐵⃗ pointing in the +z-direction. A conducting loop PQR, in the form of an equilateral triangle of the same height 𝐿, is placed in the x-y plane with its vertex P at x = 0 in the orientation shown in the figure. At 𝑡 = 0, the loop starts entering the region of the magnetic field with a uniform velocity 𝑣 along the +x-direction. The plane of the loop and its orientation remain unchanged throughout its motion.
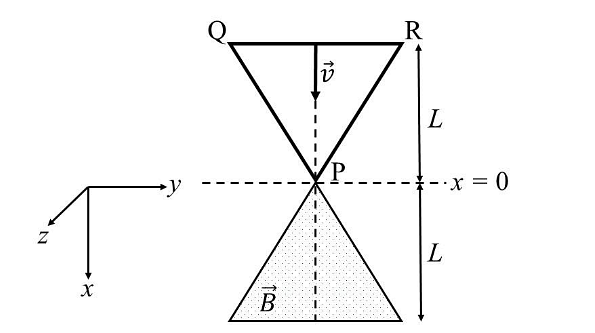
Which of the following graph best depicts the variation of the induced emf (E) in the loop as a function of the distance (𝑥) starting from 𝑥 = 0? - Two beads, each with charge q and mass m, are on a horizontal, frictionless, non-conducting, circular hoop of radius R. One of the beads is glued to the hoop at some point, while the other one performs small oscillations about its equilibrium position along the hoop. The square of the angular frequency of the small oscillations is given by [ \(\epsilon_0 \)is the permittivity of free space.]
- JEE Advanced - 2024
- Moving charges and magnetism
- A group of 9 students, s1, s2,…., s9, is to be divided to form three teams X, Y and Z of sizes 2, 3, and 4, respectively. Suppose that s1 cannot be selected for the team X and s2 cannot be selected for the team Y. Then the number of ways to form such teams, is _______.
- JEE Advanced - 2024
- Combinations
- Let \(\vec{p}=2\hat{i}+\hat{j}+3\hat{k}\) and \(\vec{q}=\hat{i}-\hat{j}+\hat{k}\). If for some real numbers α, β and γ we have
\(15\hat{i}+10\hat{j}+6\hat{k}=α(2\vec{p}+\vec{q})+β(\vec{p}-2\vec{q})+γ(\vec{p}\times\vec{q})\),
then the value of γ is ________.- JEE Advanced - 2024
- Vector Algebra
- Let X be a random variable, and let P(X = x) denote the probability that X takes the value x. Suppose that the points (x, P(X = x)), x = 0,1,2,3,4, lie on a fixed straight line in the xy -plane, and P(X = x) = 0 for all x ∈ R - {0,1,2,3,4}. If the mean of X is \(\frac{5}{2}\) , and the variance of X is α, then the value of 24α is ______.
- JEE Advanced - 2024
- Probability
Concepts Used:
Arithmetic Progression
Arithmetic Progression (AP) is a mathematical series in which the difference between any two subsequent numbers is a fixed value.
For example, the natural number sequence 1, 2, 3, 4, 5, 6,... is an AP because the difference between two consecutive terms (say 1 and 2) is equal to one (2 -1). Even when dealing with odd and even numbers, the common difference between two consecutive words will be equal to 2.
In simpler words, an arithmetic progression is a collection of integers where each term is resulted by adding a fixed number to the preceding term apart from the first term.
For eg:- 4,6,8,10,12,14,16
We can notice Arithmetic Progression in our day-to-day lives too, for eg:- the number of days in a week, stacking chairs, etc.
Read More: Sum of First N Terms of an AP



