The probabilities that a student passes in Mathematics, Physics and Chemistry are m, p and c, respectively. Of these subjects, the students has a 75% chance of passing in at least one, a 50% chance of passing in at least two and a 40% chance of passing in exactly two. Which of the following relations are true
- p + m + c =$\frac{19}{20}$
- p + m + c =$\frac{27}{20}$
- pmc=$\frac{1}{10}$
- pmc=$\frac{1}{4}$
The Correct Option is C
Solution and Explanation
student passes in Maths, Physics and Chemistry.
It is given,
$P(A) = m, P(B) = p$ and $P(C) = c$ and P (passing atleast in one subject)
$\hspace30mm =P(A \cup B \cup C)=0.75 $
$\Rightarrow \, \, \, \, 1-P(A' \cap B' \cap C')=0.75$
$\because \, \, \, \, \, \, \, \, \, \, \, \, \, \, [P(A)=1-P(\overline{A}) $
and $ \, \, \, \, \, \, \, \, [P\overline{(A \cup B \cup C)}]=P(A' \cap B' \cap C')]$
$\Rightarrow \, \, \, \, \, \, \, \, \, 1-P(A').P(B').P(C')=0.75$
$\therefore \, A, B$ and $C$ are independent events, therefore $A', B' $ and $C $' are independent events.
$\Rightarrow \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, 0.75=1-(1-m)(1-q)(1-c)$
$\Rightarrow \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, 0.25=(1-m)(1-q)(1-c) $
...(i)
Also, P (passing exactly in two subj|ects)= 0.4
$\Rightarrow \, P(A \cap B \cap \overline{C} \cup \, A \cap \overline{B} \cap C \cup \overline{A} \cap B \cap C)= 0.4$
$\Rightarrow \, \, P(A \cap B \cap \overline{C}) +\, P(A \cap \overline{B} \cap C ) + \, P(\overline{A} \cap B \cap C)=0.4$
$\Rightarrow \, \, P(A)P(B)P(\overline{C})+P(A)P(\overline{B})P(C)$
$\hspace30mm + P(\overline{A}) P(B) P(C)= 0.4$
$\Rightarrow \, \, pm (1 - c) + p(1 - m) c + (1 - p) mc = 0.4 $
$\Rightarrow \, \, pm - pmc + pc - pmc + mc - pmc = 0.4 ...$(ii)
Again, P (passing atleast in two subjects) = 0.5
$\hspace30mm + P(\overline{A}) P(B) P(C)= 0.4$
$\Rightarrow \, \, \, pm(1 - c) + pc(1 -m )+ cm( 1 - p) + pcm = 0.5$
$\Rightarrow \, \, \, pm - pcmn + p c - pcm + cm - pcm + pcm = 0.5 $
$\Rightarrow \, \, \, (pm + pc + me ) -2pcm =0.5 ...........$(iii)
From E (ii),
$\hspace20mm pm+ pc+ mc-3pcm =0.4 ...$(iv)
From E (i),
$025 = 1 - (m + p + c )+ (pm + pc + cm) - pcm ........... $.(v)
On solving Eqs. (iii), (iv) and (v), we get
$\hspace20mm p + m + c= 1.35 = 27/20$
Therefore, option (b) is correct.
Also, from Eqs. (ii) and (iii), we get pmc= 1/10
Hence, option (c) is correct.
Top Questions on Probability
- Let Ajay will not appear in JEE exam with probability $p = \frac{2}{7}$, while both Ajay and Vijay will appear in the exam with probability $q = \frac{1}{5}$. Then the probability that Ajay will appear in the exam and Vijay will not appear is:
- JEE Main - 2024
- Mathematics
- Probability
- A company has two plants A and B to manufacture motorcycles. 60% motorcycles are manufactured at plant A and the remaining are manufactured at plant B. 80% of the motorcycles manufactured at plant A are rated of the standard quality, while 90% of the motorcycles manufactured at plant B are rated of the standard quality. A motorcycle picked up randomly from the total production is found to be of the standard quality. If p is the probability that it was manufactured at plant B, then 126p is
- JEE Main - 2024
- Mathematics
- Probability
- If three letters can be posted to any one of the 5 different addresses, then the probability that the three letters are posted to exactly two addresses is:
- JEE Main - 2024
- Mathematics
- Probability
- The coefficients a, b, c in the quadratic equation ax2 + bx + c = 0 are from the set {1, 2, 3, 4, 5, 6}. If the probability of this equation having one real root bigger than the other is p, then 216p equals :
- JEE Main - 2024
- Mathematics
- Probability
- Three urns A, B and C contain 7 red, 5 black; 5 red, 7 black and 6 red, 6 black balls, respectively. One of the urn is selected at random and a ball is drawn from it. If the ball drawn is black, then then probability that it is drawn from urn A is :
- JEE Main - 2024
- Mathematics
- Probability
Questions Asked in JEE Advanced exam
- A closed vessel contains 10 g of an ideal gas X at 300 K, which exerts 2 atm pressure. At the same temperature, 80 g of another ideal gas Y is added to it and the pressure becomes 6 atm. The ratio of root mean square velocities of X and Y at 300 K is
- JEE Advanced - 2024
- States of matter
- Let the function \(f:[1,\infin)→\R\) be defined by
\(f(t) = \begin{cases} (-1)^{n+1}2, & \text{if } t=2n-1,n\in\N, \\ \frac{(2n+1-t)}{2}f(2n-1)+\frac{(t-(2n-1))}{2}f(2n+1) & \text{if } 2n-1<t<2n+1,n\in\N. \end{cases}\)
Define \(g(x)=\int\limits_{1}^{x}f(t)dt,x\in(1,\infin).\) Let α denote the number of solutions of the equation g(x) = 0 in the interval (1, 8] and \(β=\lim\limits_{x→1+}\frac{g(x)}{x-1}\). Then the value of α + β is equal to _____.- JEE Advanced - 2024
- Integral Calculus
- A dimensionless quantity is constructed in terms of electronic charge \(e\), permittivity of free space \(\epsilon_0\) , Planck’s constant ℎ, and speed of light c. If the dimensionless quantity is written as \(e^\alpha\epsilon_0^\beta h^\gamma c^\delta\)and n is a non-zero integer, then\((\alpha, \beta,\gamma,\delta)\) is given by
- JEE Advanced - 2024
- Semiconductor electronics: materials, devices and simple circuits
- A block of mass \(5 kg\) moves along the \(x-\)direction subject to the force \(F = (−20x + 10) N,\) with the value of \(x \) in metre. At time \(t = 0 s,\) it is at rest at position \(x = 1 m\). The position and momentum of the block at \(t = (\pi/4)\) s are
- JEE Advanced - 2024
- Work-energy theorem
- A region in the form of an equilateral triangle (in x-y plane) of height L has a uniform magnetic field 𝐵⃗ pointing in the +z-direction. A conducting loop PQR, in the form of an equilateral triangle of the same height 𝐿, is placed in the x-y plane with its vertex P at x = 0 in the orientation shown in the figure. At 𝑡 = 0, the loop starts entering the region of the magnetic field with a uniform velocity 𝑣 along the +x-direction. The plane of the loop and its orientation remain unchanged throughout its motion.
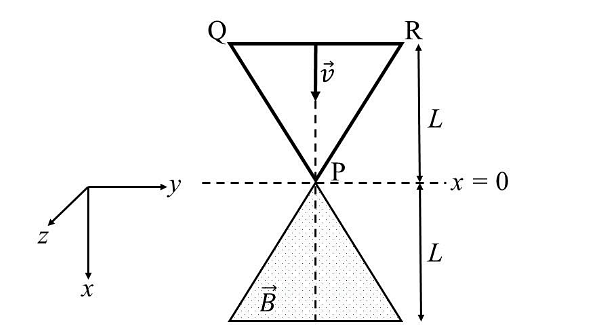
Which of the following graph best depicts the variation of the induced emf (E) in the loop as a function of the distance (𝑥) starting from 𝑥 = 0?
Concepts Used:
Probability
Probability is defined as the extent to which an event is likely to happen. It is measured by the ratio of the favorable outcome to the total number of possible outcomes.
The definitions of some important terms related to probability are given below:
Sample space
The set of possible results or outcomes in a trial is referred to as the sample space. For instance, when we flip a coin, the possible outcomes are heads or tails. On the other hand, when we roll a single die, the possible outcomes are 1, 2, 3, 4, 5, 6.
Sample point
In a sample space, a sample point is one of the possible results. For instance, when using a deck of cards, as an outcome, a sample point would be the ace of spades or the queen of hearts.
Experiment
When the results of a series of actions are always uncertain, this is referred to as a trial or an experiment. For Instance, choosing a card from a deck, tossing a coin, or rolling a die, the results are uncertain.
Event
An event is a single outcome that happens as a result of a trial or experiment. For instance, getting a three on a die or an eight of clubs when selecting a card from a deck are happenings of certain events.
Outcome
A possible outcome of a trial or experiment is referred to as a result of an outcome. For instance, tossing a coin could result in heads or tails. Here the possible outcomes are heads or tails. While the possible outcomes of dice thrown are 1, 2, 3, 4, 5, or 6.



