Question:
The point of intersection $C$ of the plane $8 x+y+2 z=0$ and the line joining the points $A (-3,-6,1)$ and $B (2,4,-3)$ divides the line segment $AB$ internally in the ratio $k : 1$ If $a , b , c (| a |,| b |$, $| c |$ are coprime) are the direction ratios of the perpendicular from the point $C$ on the line $\frac{1-x}{1}=\frac{y+4}{2}=\frac{z+2}{3}$, then $| a + b + c |$ is equal to ___
The point of intersection $C$ of the plane $8 x+y+2 z=0$ and the line joining the points $A (-3,-6,1)$ and $B (2,4,-3)$ divides the line segment $AB$ internally in the ratio $k : 1$ If $a , b , c (| a |,| b |$, $| c |$ are coprime) are the direction ratios of the perpendicular from the point $C$ on the line $\frac{1-x}{1}=\frac{y+4}{2}=\frac{z+2}{3}$, then $| a + b + c |$ is equal to ___
Updated On: Oct 1, 2024
Hide Solution
Verified By Collegedunia
Correct Answer: 10
Solution and Explanation
The correct answer is 10.
Plane :
Given line
Any point on line
Point of intersection of line and plane
Plane :
Given line
Any point on line
Point of intersection of line and plane

Was this answer helpful?
0
0
Top Questions on Three Dimensional Geometry
- A straight line drawn from the point P(1,3, 2), parallel to the line \(\frac{x-2}{1}=\frac{y-4}{2}=\frac{z-6}{1}\), intersects the plane L1 : x - y + 3z = 6 at the point Q. Another straight line which passes through Q and is perpendicular to the plane L1 intersects the plane L2 : 2x - y + z = -4 at the point R. Then which of the following statements is (are) TRUE ?
- JEE Advanced - 2024
- Mathematics
- Three Dimensional Geometry
- Let y ∈ R be such that the lines \(L_1:\frac{x+11}{1}=\frac{y+21}{2}=\frac{z+29}{3}\) and \(L_2:\frac{x+16}{3}=\frac{y+11}{2}=\frac{z+4}{\gamma}\) intersect. Let R1 be the point of intersection of L1 and L2. Let O = (0, 0 ,0), and \(\hat{n}\) denote a unit normal vector to the plane containing both the lines L1 and L2.
Match each entry in List-I to the correct entry in List-II.The correct option isList - I List - II (P) γ equals (1) \(-\hat{i}-\hat{j}+\hat{k}\) (Q) A possible choice for \(\hat{n}\) is (2) \(\sqrt{\frac{3}{2}}\) (R) \(\overrightarrow{OR_1}\) equals (3) 1 (S) A possible value of \(\overrightarrow{OR_1}.\hat{n}\) is (4) \(\frac{1}{\sqrt6}\hat{i}-\frac{2}{\sqrt6}\hat{j}+\frac{1}{\sqrt6}\hat{k}\) (5) \(\sqrt{\frac{2}{3}}\) - JEE Advanced - 2024
- Mathematics
- Three Dimensional Geometry
- Let R3 denote the three-dimensional space. Take two points P = (1, 2, 3) and Q = (4, 2 ,7). Let
dist(X, Y) denote the distance between two points X and Y in R3. Let
\(S=\left\{X\in\R^3:(dist(X,P)^2)-(dist(X,Q))^2=50\right\}\ and\)
\(T=\left\{Y\in \R^3:(dist(Y,Q))^2-(dist(Y,P))^2=50\right\}\)
Then which of the following statements is (are) TRUE ?- JEE Advanced - 2024
- Mathematics
- Three Dimensional Geometry
- If the foot is perpendicular from (1, 2, 3) to the line \(\frac{x+1}{2} = \frac{y-2}{5} = \frac{z-1}{1}\) is \(( a, \beta, \gamma)\), then find \(a + \beta + \gamma\)
- JEE Main - 2024
- Mathematics
- Three Dimensional Geometry
- Let the line / : x = \(\frac{1-y}{2}=\frac{z-3}{\lambda}, \lambda \in R\) meet the plane P : x+2y +3z = 4 at the point \((\alpha, \beta, \lambda)\). If the angle between the line I and the plane P is \(cos^{-1}\bigg(\sqrt{\frac{5}{14}}\bigg)\) then \(\alpha+2\beta+6\lambda\) is equal to______.
- JEE Main - 2023
- Mathematics
- Three Dimensional Geometry
View More Questions
Questions Asked in JEE Main exam
- Find the acceleration of \(2\) \(kg\) block shown in the diagram (neglect friction)

- JEE Main - 2024
- Acceleration
- If \(|2A|^3 =21\) and \(\begin{bmatrix} 1 & 0 & 0 \\[0.3em] 0 & α & β \\[0.3em] 0 & β & α \end{bmatrix}\), then a is (if \(α,β∈I\))
- JEE Main - 2024
- Matrices
- Let \(α\) and \(β\) the roots of equation \(px^2 + qx - r = 0\), where \(P≠ 0\). If \(p,q,r\) be the consecutive term of non constant G.P and \(\frac{1}{α} + \frac{1}{β} = \frac{3}{4}\) then the value of \((α - β)^2\) is:
- JEE Main - 2024
- Geometric Progression
- Two lines \(L_1 \;\& \;L_2\) passing through origin trisecting the line segment intercepted by the line \(4x + 5y = 20\) between the coordinate axes. Then the tangent of angle between the lines \(L_1\) and \(L_2\) is
- JEE Main - 2024
- Tangents and Normals
- Rank of the word 'GTWENTY' in dictionary is _____ .
- JEE Main - 2024
- permutations and combinations
View More Questions
Concepts Used:
Three Dimensional Geometry
Mathematically, Geometry is one of the most important topics. The concepts of Geometry are derived w.r.t. the planes. So, Geometry is divided into three major categories based on its dimensions which are one-dimensional geometry, two-dimensional geometry, and three-dimensional geometry.
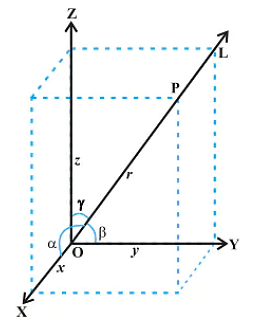
Direction Cosines and Direction Ratios of Line:
Consider a line L that is passing through the three-dimensional plane. Now, x,y and z are the axes of the plane and α,β, and γ are the three angles the line makes with these axes. These are commonly known as the direction angles of the plane. So, appropriately, we can say that cosα, cosβ, and cosγ are the direction cosines of the given line L.