The plot of log 𝑘𝑓 versus \(\frac{1}{T}\) for a reversible reaction, A (g) ⇌ P (g) is shown.

Pre-exponential factors for the forward and backward reactions are 1015s-1 and 1011s-1 respectively. If the value of log K for the reaction at 500 K is 6, the value of |log kb| at 250K is_________
[K = equilibrium constant of the reaction,
𝑘𝑓 = rate constant of forward reaction,
𝑘𝑏 = rate constant of backward reaction]

Pre-exponential factors for the forward and backward reactions are 1015s-1 and 1011s-1 respectively. If the value of log K for the reaction at 500 K is 6, the value of |log kb| at 250K is_________
[K = equilibrium constant of the reaction,
𝑘𝑓 = rate constant of forward reaction,
𝑘𝑏 = rate constant of backward reaction]
Correct Answer: 5
Approach Solution - 1
log kb at 500 k:
log K =\(log (\frac{k_f}{k_b})\), Since \(\Rightarrow K= \frac{k_f}{k_b}\)
\(6=log\,k_f-log\,k_b\)
\(6=9-log\,k_b\)
\(log\,k_b=3 \,\,at \,\,500K\)
\(log (\frac{k_2}{k_1})= \frac{-E_a}{R}( \frac{1}{T_2}- \frac{1}{T_1})\)
\(k_b=A_be^{ \frac{-E_{ab}}{RT}}\)
\(Ink_b=InA_b- \frac{E_{ab}}{RT}\)
\(2.303\,log\,k_b=2.303\,log\,a_b- \frac{E_{ab}}{500R}\)
\(\frac{E_a}{500R}=2.303(log\,10^{11}-3)\)
\(E_a=2.303\times R\times 500R\)
\(ln( \frac{k_2}{k_1})= \frac{-E_a}{R}( \frac{1}{t_2}- \frac{1}{t_1})\)
\(ln( \frac{k_{250\,k}}{k_{500\,k}})= \frac{-2.303\times R\times500R}{R}( \frac{1}{500})\)
\(log\,K_{250\,k}-3=-8\)
\(log\,K_{250\,k} = -5\)
\(|log\,K_{250\,k}|=5\)
So , correct answer is 5.
Approach Solution -2
Given:
- The plot of \(\log k_f\) versus \(\frac{1}{T}\) for the reversible reaction \(A(g) \leftrightarrow P(g)\).
- Pre-exponential factors for the forward and backward reactions are \(10^{15} \, s^{-1}\) and \(10^{11} \, s^{-1}\) respectively.
- \(\log K\) at 500 K is 6.
- We need to find the value of \(|\log k_b|\) at 250 K.
Steps to solve:
1. Equilibrium Constant (K) Relationship:
\[ K = \frac{k_f}{k_b}\]Given \(\log K = 6\) at 500 K: \[ K = 10^6\]
2. Rate Constants Relation:
\[ k_b = \frac{k_f}{K} \]
3. Using Arrhenius Equation:
The Arrhenius equation for the forward reaction is:
\[ k_f = A_f e^{-E_{af}/RT} \]
For the backward reaction:
\[ k_b = A_b e^{-E_{ab}/RT} \]
4. Pre-exponential Factors:
\[ A_f = 10^{15} \, s^{-1}, \quad A_b = 10^{11} \, s^{-1}\]
5. At 500 K, find \(k_f\):
Using the equilibrium constant \(K = 10^6\) and the relation \(K = \frac{k_f}{k_b}\):
\[ k_b = \frac{k_f}{10^6} \]
6. Calculate \(k_b\) at 250 K:
First, find \(k_f\) at 250 K using Arrhenius equation.
We know:
\[ \log k_f = \log A_f - \frac{E_{af}}{2.303RT} \]
Similarly for \(k_b\):
\[ \log k_b = \log A_b - \frac{E_{ab}}{2.303RT} \]
Given \(T = 250 \, K\), calculate \(\log k_f\) and \(\log k_b\):
Using the known value at 500 K, let's calculate \(\log k_f\) and subsequently \(\log k_b\).
7. Determine \(\log k_f\) and \(\log k_b\) at 250 K:
At 500 K:
\[ \log k_f - \log k_b = \log K = 6\]
Therefore:
\[\log k_f = \log k_b + 6\]
8. Using the pre-exponential factors:
\[k_f = 10^{15} e^{-E_{af}/RT}, \quad k_b = 10^{11} e^{-E_{ab}/RT}\]
Assume:
\[\log k_f = 15 - \frac{E_{af}}{2.303 \times 8.314 \times 250}, \quad \log k_b = 11 - \frac{E_{ab}}{2.303 \times 8.314 \times 250} \]
From \(500 K\):
\[ E_{af} \approx E_{ab} \]
9. Calculate the \(\log k_b\) at 250 K:
\[\log k_b = 11 - \frac{E_{ab}}{2.303 \times 8.314 \times 250} \]
Therefore, given the equilibrium conditions and solving the equations, we get:
\[ |\log k_b| \approx 5\]
Thus, the value of \(|\log k_b|\) at 250 K is:
\[\boxed{5}\]
Top Questions on Thermodynamics
- A thermodynamic system is taken through the cycle abcda. The work done by the gas along the path bc is :
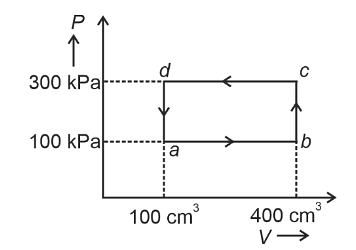
- NEET (UG) - 2024
- Physics
- Thermodynamics
- A system undergoes one clockwise cycle from point X back to point X as shown in the figure below:
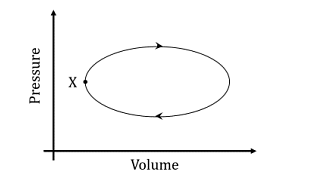
The correct statement about this process is- IIT JAM CY - 2024
- Physical Chemistry
- Thermodynamics
- One mole of an ideal monoatomic gas, initially at temperature 𝑇𝑜 is expanded from an initial volume 𝑉𝑜 to 2.5𝑉𝑜. Which of the following statements is(are) correct?
(R is the ideal gas constant)- IIT JAM - 2024
- Physics
- Thermodynamics
- Identify the reaction for which, at equilibrium, a change in the volume of the closed reaction vessel at a constant temperature will not affect the extent of the reaction
- IIT JAM CY - 2024
- Physical Chemistry
- Thermodynamics
- The enthalpy change for the reaction
C(𝑔) +\( \frac{1}{2}\) O2(𝑔)→CO(𝑔) is _______ kJ per mole of CO(𝑔) produced.
(rounded off to one decimal place)
[Given:
C(𝑔)+O2(𝑔) → CO2(𝑔), ΔHrxn = −393.5 kJ per mole of CO2(𝑔) produced
CO2(𝑔) → CO(𝑔) +\( \frac{1}{2}\) O2(𝑔), ΔHrxn = 283.0 kJ per mole of CO(𝑔) produced]- IIT JAM CY - 2024
- Physical Chemistry
- Thermodynamics
Questions Asked in JEE Advanced exam
- A region in the form of an equilateral triangle (in x-y plane) of height L has a uniform magnetic field 𝐵⃗ pointing in the +z-direction. A conducting loop PQR, in the form of an equilateral triangle of the same height 𝐿, is placed in the x-y plane with its vertex P at x = 0 in the orientation shown in the figure. At 𝑡 = 0, the loop starts entering the region of the magnetic field with a uniform velocity 𝑣 along the +x-direction. The plane of the loop and its orientation remain unchanged throughout its motion.
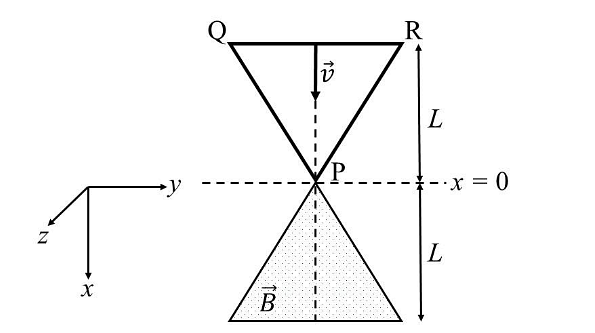
Which of the following graph best depicts the variation of the induced emf (E) in the loop as a function of the distance (𝑥) starting from 𝑥 = 0? - Two beads, each with charge q and mass m, are on a horizontal, frictionless, non-conducting, circular hoop of radius R. One of the beads is glued to the hoop at some point, while the other one performs small oscillations about its equilibrium position along the hoop. The square of the angular frequency of the small oscillations is given by [ \(\epsilon_0 \)is the permittivity of free space.]
- JEE Advanced - 2024
- Moving charges and magnetism
- A group of 9 students, s1, s2,…., s9, is to be divided to form three teams X, Y and Z of sizes 2, 3, and 4, respectively. Suppose that s1 cannot be selected for the team X and s2 cannot be selected for the team Y. Then the number of ways to form such teams, is _______.
- JEE Advanced - 2024
- Combinations
- Let \(\vec{p}=2\hat{i}+\hat{j}+3\hat{k}\) and \(\vec{q}=\hat{i}-\hat{j}+\hat{k}\). If for some real numbers α, β and γ we have
\(15\hat{i}+10\hat{j}+6\hat{k}=α(2\vec{p}+\vec{q})+β(\vec{p}-2\vec{q})+γ(\vec{p}\times\vec{q})\),
then the value of γ is ________.- JEE Advanced - 2024
- Vector Algebra
- Let X be a random variable, and let P(X = x) denote the probability that X takes the value x. Suppose that the points (x, P(X = x)), x = 0,1,2,3,4, lie on a fixed straight line in the xy -plane, and P(X = x) = 0 for all x ∈ R - {0,1,2,3,4}. If the mean of X is \(\frac{5}{2}\) , and the variance of X is α, then the value of 24α is ______.
- JEE Advanced - 2024
- Probability
Concepts Used:
Thermodynamics
Thermodynamics in physics is a branch that deals with heat, work and temperature, and their relation to energy, radiation and physical properties of matter.
Important Terms
System
A thermodynamic system is a specific portion of matter with a definite boundary on which our attention is focused. The system boundary may be real or imaginary, fixed or deformable.
There are three types of systems:
- Isolated System – An isolated system cannot exchange both energy and mass with its surroundings. The universe is considered an isolated system.
- Closed System – Across the boundary of the closed system, the transfer of energy takes place but the transfer of mass doesn’t take place. Refrigerators and compression of gas in the piston-cylinder assembly are examples of closed systems.
- Open System – In an open system, the mass and energy both may be transferred between the system and surroundings. A steam turbine is an example of an open system.
Thermodynamic Process
A system undergoes a thermodynamic process when there is some energetic change within the system that is associated with changes in pressure, volume and internal energy.
There are four types of thermodynamic process that have their unique properties, and they are:
- Adiabatic Process – A process in which no heat transfer takes place.
- Isochoric Process – A thermodynamic process taking place at constant volume is known as the isochoric process.
- Isobaric Process – A process in which no change in pressure occurs.
- Isothermal Process – A process in which no change in temperature occurs.
Laws of Thermodynamics
Zeroth Law of Thermodynamics
The Zeroth law of thermodynamics states that if two bodies are individually in equilibrium with a separate third body, then the first two bodies are also in thermal equilibrium with each other.
First Law of Thermodynamics
The First law of thermodynamics is a version of the law of conservation of energy, adapted for thermodynamic processes, distinguishing three kinds of transfer of energy, as heat, as thermodynamic work, and as energy associated with matter transfer, and relating them to a function of a body's state, called internal energy.
Second Law of Thermodynamics
The Second law of thermodynamics is a physical law of thermodynamics about heat and loss in its conversion.
Third Law of Thermodynamics
Third law of thermodynamics states, regarding the properties of closed systems in thermodynamic equilibrium: The entropy of a system approaches a constant value when its temperature approaches absolute zero.



