The number of diagonals of a polygon is 35. If A, B are two distinct vertices of this polygon, then the number of all those triangles formed by joining three vertices of the polygon having AB as one of its sides is:
The number of diagonals of a polygon is 35. If A, B are two distinct vertices of this polygon, then the number of all those triangles formed by joining three vertices of the polygon having AB as one of its sides is:
1
8
10
12
The Correct Option is C
Solution and Explanation
The correct option is: (C) 10.
Number of diagonals=2n(n−3)
Given that the number of diagonals is 35, we can set up an equation and solve for n:
n(n−3)=70
Now, we need to find two integers n and n−3 whose product is 70. The pairs of integers that satisfy this condition are (n,n−3)=(10,7) and (−3)=(35,32)(n,n−3)=(35,32).
However, in the context of a polygon, the number of sides cannot be negative or zero, so we discard the solution(n,n−3)=(35,32).
Therefore, the number of sides of the polygon is n=10.
Top Questions on Three Dimensional Geometry
- A straight line drawn from the point P(1,3, 2), parallel to the line \(\frac{x-2}{1}=\frac{y-4}{2}=\frac{z-6}{1}\), intersects the plane L1 : x - y + 3z = 6 at the point Q. Another straight line which passes through Q and is perpendicular to the plane L1 intersects the plane L2 : 2x - y + z = -4 at the point R. Then which of the following statements is (are) TRUE ?
- JEE Advanced - 2024
- Mathematics
- Three Dimensional Geometry
- Let y ∈ R be such that the lines \(L_1:\frac{x+11}{1}=\frac{y+21}{2}=\frac{z+29}{3}\) and \(L_2:\frac{x+16}{3}=\frac{y+11}{2}=\frac{z+4}{\gamma}\) intersect. Let R1 be the point of intersection of L1 and L2. Let O = (0, 0 ,0), and \(\hat{n}\) denote a unit normal vector to the plane containing both the lines L1 and L2.
Match each entry in List-I to the correct entry in List-II.The correct option isList - I List - II (P) γ equals (1) \(-\hat{i}-\hat{j}+\hat{k}\) (Q) A possible choice for \(\hat{n}\) is (2) \(\sqrt{\frac{3}{2}}\) (R) \(\overrightarrow{OR_1}\) equals (3) 1 (S) A possible value of \(\overrightarrow{OR_1}.\hat{n}\) is (4) \(\frac{1}{\sqrt6}\hat{i}-\frac{2}{\sqrt6}\hat{j}+\frac{1}{\sqrt6}\hat{k}\) (5) \(\sqrt{\frac{2}{3}}\) - JEE Advanced - 2024
- Mathematics
- Three Dimensional Geometry
- Let R3 denote the three-dimensional space. Take two points P = (1, 2, 3) and Q = (4, 2 ,7). Let
dist(X, Y) denote the distance between two points X and Y in R3. Let
\(S=\left\{X\in\R^3:(dist(X,P)^2)-(dist(X,Q))^2=50\right\}\ and\)
\(T=\left\{Y\in \R^3:(dist(Y,Q))^2-(dist(Y,P))^2=50\right\}\)
Then which of the following statements is (are) TRUE ?- JEE Advanced - 2024
- Mathematics
- Three Dimensional Geometry
- If the foot is perpendicular from (1, 2, 3) to the line \(\frac{x+1}{2} = \frac{y-2}{5} = \frac{z-1}{1}\) is \(( a, \beta, \gamma)\), then find \(a + \beta + \gamma\)
- JEE Main - 2024
- Mathematics
- Three Dimensional Geometry
- Let the line / : x = \(\frac{1-y}{2}=\frac{z-3}{\lambda}, \lambda \in R\) meet the plane P : x+2y +3z = 4 at the point \((\alpha, \beta, \lambda)\). If the angle between the line I and the plane P is \(cos^{-1}\bigg(\sqrt{\frac{5}{14}}\bigg)\) then \(\alpha+2\beta+6\lambda\) is equal to______.
- JEE Main - 2023
- Mathematics
- Three Dimensional Geometry
Questions Asked in TS EAMCET exam
If A is a square matrix of order 3, then |Adj(Adj A2)| =
- TS EAMCET - 2023
- Algebra of Complex Numbers
Match the following List -I (Complex) List II (Spin only Magnetic Moment)
List -I (Complex) List II (Spin only Magnetic Moment) A) [CoF6]3- I) 0 B) [Co(C2O4)3]3- II) √24 C) [FeF6]3+ III) √8 D) [Mn(CN)6]3- IV) √35 V) √15 the correct answer is:
- TS EAMCET - 2023
- coordination compounds
If (h,k) is the image of the point (3,4) with respect to the line 2x - 3y -5 = 0 and (l,m) is the foot of the perpendicular from (h,k) on the line 3x + 2y + 12 = 0, then lh + mk + 1 = 2x - 3y - 5 = 0.
- TS EAMCET - 2023
- Coordinate Geometry
If a line ax + 2y = k forms a triangle of area 3 sq.units with the coordinate axis and is perpendicular to the line 2x - 3y + 7 = 0, then the product of all the possible values of k is
- TS EAMCET - 2023
- Algebra of Complex Numbers
- If the solution of the differential equation \(\frac{dy}{dx}=\frac{2x+3y}{3x-2y}\) is y = xtan(f(x)) + c then f(x) =
- TS EAMCET - 2023
- Differential equations
Concepts Used:
Three Dimensional Geometry
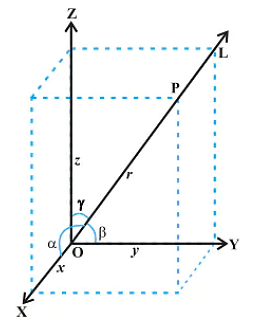
Mathematically, Geometry is one of the most important topics. The concepts of Geometry are derived w.r.t. the planes. So, Geometry is divided into three major categories based on its dimensions which are one-dimensional geometry, two-dimensional geometry, and three-dimensional geometry.
Direction Cosines and Direction Ratios of Line:
Consider a line L that is passing through the three-dimensional plane. Now, x,y and z are the axes of the plane and α,β, and γ are the three angles the line makes with these axes. These are commonly known as the direction angles of the plane. So, appropriately, we can say that cosα, cosβ, and cosγ are the direction cosines of the given line L.