Select Goal &
City
Select Goal
Explore
Question:
The modulus of the complex number \(\frac{(1+i)^2(1+3i)}{(2-6i)(2-2i)}\) is
The modulus of the complex number \(\frac{(1+i)^2(1+3i)}{(2-6i)(2-2i)}\) is
Updated On: Nov 21, 2024
- \(\frac{1}{\sqrt2}\)
- \(\frac{4}{\sqrt2}\)
- \(\frac{\sqrt2}{4}\)
- \(\frac{2}{\sqrt2}\)
Hide Solution
Verified By Collegedunia
The Correct Option is C
Solution and Explanation
The correct answer is (C) : \(\frac{\sqrt2}{4}\).
Was this answer helpful?
10
9
Top Questions on complex numbers
- Consider the following two statements:
Statement I: For any two non-zero complex numbers \( z_1, z_2 \),
\((|z_1| + |z_2|) \left| \frac{z_1}{|z_1|} + \frac{z_2}{|z_2|} \right| \leq 2 (|z_1| + |z_2|)\)
Statement II: If \( x, y, z \) are three distinct complex numbers and \( a, b, c \) are three positive real numbers such that
\(\frac{a}{|y - z|} = \frac{b}{|z - x|} = \frac{c}{|x - y|},\)
then
\(\frac{a^2}{y - z} + \frac{b^2}{z - x} + \frac{c^2}{x - y} = 1.\)
Between the above two statements,- JEE Main - 2024
- Mathematics
- complex numbers
- If \( \alpha \) denotes the number of solutions of \( |1 - i|^x = 2^x \) and \( \beta = \frac{|z|}{\arg(z)} \), where \[ z = \frac{\pi}{4} (1 + i)^4 \left( \frac{1 - \sqrt{\pi} i}{\sqrt{\pi} + i} + \frac{\sqrt{\pi} - i}{1 + \sqrt{\pi} i} \right), \quad i = \sqrt{-1}, \] then the distance of the point \( (\alpha, \beta) \) from the line \( 4x - 3y = 7 \) is _____
- JEE Main - 2024
- Mathematics
- complex numbers
- Let \( \alpha, \beta \) be the roots of the equation \( x^2 - x + 2 = 0 \) with \( \text{Im}(\alpha) > \text{Im}(\beta) \). Then \( \alpha^6 + \alpha^4 + \beta^4 - 5 \alpha^2 \) is equal to
- JEE Main - 2024
- Mathematics
- complex numbers
- Let \( z_1 \) and \( z_2 \) be two complex numbers such that \( z_1 + z_2 = 5 \) and \( z_1^3 + z_2^3 = 20 + 15i \). Then \( \left| z_1^4 + z_2^4 \right| \) equals
- JEE Main - 2024
- Mathematics
- complex numbers
- Let \( z \) be a complex number such that the real part of \[ \frac{z - 2i}{z + 2i} \] is zero. Then, the maximum value of \( |z - (6 + 8i)| \) is equal to:
- JEE Main - 2024
- Mathematics
- complex numbers
View More Questions
Questions Asked in KCET exam
- The P-V diagram of a Carnot's engine is shown in the graph below. The engine uses 1 mole of an ideal gas as working substance. From the graph, the area enclosed by the P-V diagram is
[ The heat supplied to the gas is 8000 J ]
- KCET - 2023
- carnot cycle
- A point object is moving at a constant speed of 1 ms-1 along the principal axis of a convex lens of focal length 10cm. The speed of the image is also 1 ms-1 , when the object is at _______ cm from the optic centre of the lens.
- KCET - 2023
- spherical lenses
- A cubical Gaussian surface has side of length a = 10 cm. Electric field lines are parallel to x-axis as shown. The magnitudes of electric fields through surfaces ABCD and EFGH are 6kNC-1 and 9kNC-1 respectively. Then the total charge enclosed by the cube is
[Take ε0 = 9 × 10-12 Fm-1]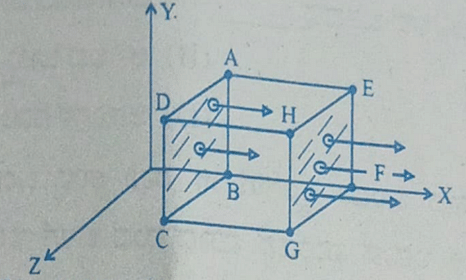
- KCET - 2023
- Gauss Law
- The value of \(\begin{vmatrix} \sin^2 14 \degree & \sin^2 66\degree & \tan 135\degree \\ \sin^2 66\degree & \tan 135\degree & \sin^2 14 \degree \\ \tan 135\degree & \sin^2 14 \degree & \sin^2 66\degree \end{vmatrix}\)
- KCET - 2023
- Trigonometric Identities
- In the Young’s double slit experiment, the intensity of light passing through each of the two double slits is 2 × 10-2 Wm-2. The screen-slit distance is very large in comparison with slit-slit distance. The fringe width is β. The distance between the central maximum and a point P on the screen is \(\frac{\beta}{3}\). Then the total light intensity at that point is
- KCET - 2023
- Youngs double slit experiment
View More Questions
SUBSCRIBE TO OUR NEWS LETTER
COLLEGE NOTIFICATIONSEXAM NOTIFICATIONSNEWS UPDATES
Download the Collegedunia app on 
© 2024 Collegedunia Web Pvt. Ltd. All Rights Reserved