Select Goal &
City
Select Goal
Explore
Question:
T$\displaystyle\lim_{x \to 0+}$ $\left(x^{n} \,ln\, x\right), n > 0$
T$\displaystyle\lim_{x \to 0+}$ $\left(x^{n} \,ln\, x\right), n > 0$
Updated On: Apr 27, 2024
- does not exist
- exists and is zero
- exists and is 1
- exists and is $e^{-1}$
Hide Solution
Verified By Collegedunia
The Correct Option is B
Solution and Explanation
$\displaystyle\lim_{x \to 0+}$$\frac{\ell nx}{\frac{1}{x^{n}}}\left(\frac{\infty}{\infty}\right).$ Applying LH rule
$\Rightarrow\, \displaystyle\lim_{x \to 0+} \frac{\frac{1}{x}}{\frac{-n}{x^{n+1}}} = 0$
$\Rightarrow\, \displaystyle\lim_{x \to 0+} \frac{\frac{1}{x}}{\frac{-n}{x^{n+1}}} = 0$
Was this answer helpful?
0
0
Top Questions on Limits
- If the domain of the function \[f(x) = \frac{\sqrt{x^2 - 25}}{(4 - x^2)} + \log_{10}(x^2 + 2x - 15)\]is $(-\infty, \alpha) \cup [\beta, \infty)$, then $\alpha^2 + \beta^3$ is equal to:
- If \[ \alpha = \lim_{x \to 0^+} \left( \frac{e^{\sqrt{\tan x}} - e^{\sqrt{x}}}{\sqrt{\tan x} - \sqrt{x}} \right) \] \[ \beta = \lim_{x \to 0} (1 + \sin x)^{\frac{1}{2\cot x}} \] are the roots of the quadratic equation \(ax^2 + bx - \sqrt{e} = 0\), then \(12 \log_e (a + b)\) is equal to _________.
- If \[ \lim_{x \to 1} \frac{(5x+1)^{1/3} - (x+5)^{1/3}}{(2x+3)^{1/2} - (x+4)^{1/2}} = \frac{m \sqrt{5}}{n (2n)^{2/3}}, \] where \( \text{gcd}(m, n) = 1 \), then \( 8m + 12n \) is equal to _____
- The value of \[ \lim_{x \to 0} 2 \left( \frac{1 - \cos x \sqrt{\cos 2x} \, \sqrt[3]{\cos 3x} \ldots \sqrt[10]{\cos 10x}}{x^2} \right) \] is _____.
- \( \lim_{x \to 0} \frac{e^{2|\sin x|} - 2|\sin x| - 1}{x^2} \)
View More Questions
Questions Asked in WBJEE exam
- Three identical convex lenses each of focal length f are placed in a straight line separated by a distance f from each other. An object is located in \(\frac{f}{2}\) in front of the leftmost lens. Then,
- WBJEE - 2023
- Ray optics and optical instruments
- A particle of mass m is projected at velocity at a velocity u, making an angle θ with the horizontal(x-axis). If the angle of projection θ is varied keeping all other parameters same, then magnitude of angular momentum(L) at its maximum height about the point of projection varies with θ as,
- WBJEE - 2023
- System of Particles & Rotational Motion
- If \(\int \frac{dx}{(x+1)(x-2)(x-3)}=\frac{1}{k}log_e\left \{ \frac{|x-3|^3|x+1|}{(x-2)^4}\right \}+c\), then the value of k is
- WBJEE - 2023
- Integrals of Some Particular Functions
- A rectangle ABCD has its side parallel to the line y=2x and vertices A,B,D are on y=1,x=1 and x=-1 respectively. The coordinate of C can be
- WBJEE - 2023
- Straight lines
- In an experiment on a circuit, as shown in the figure, the voltmeter shows 8V reading. The resistance of the voltmeter is
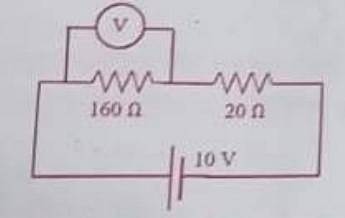
- WBJEE - 2023
- Resistance
View More Questions
Concepts Used:
Limits
A function's limit is a number that a function reaches when its independent variable comes to a certain value. The value (say a) to which the function f(x) approaches casually as the independent variable x approaches casually a given value "A" denoted as f(x) = A.
If limx→a- f(x) is the expected value of f when x = a, given the values of ‘f’ near x to the left of ‘a’. This value is also called the left-hand limit of ‘f’ at a.
If limx→a+ f(x) is the expected value of f when x = a, given the values of ‘f’ near x to the right of ‘a’. This value is also called the right-hand limit of f(x) at a.
If the right-hand and left-hand limits concur, then it is referred to as a common value as the limit of f(x) at x = a and denote it by lim x→a f(x).
SUBSCRIBE TO OUR NEWS LETTER
COLLEGE NOTIFICATIONSEXAM NOTIFICATIONSNEWS UPDATES
Download the Collegedunia app on 
© 2024 Collegedunia Web Pvt. Ltd. All Rights Reserved