Question:
Let the eccentricity of the hyperbola $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ be reciprocal to that of the ellipse $x^2+4y^2=4.$ If the
hyperbola passes through a focus of the ellipse, then
Let the eccentricity of the hyperbola $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ be reciprocal to that of the ellipse $x^2+4y^2=4.$ If the
hyperbola passes through a focus of the ellipse, then
Updated On: Jun 14, 2022
- (a) the equation of the hyperbola is $\frac{x^2}{3}-\frac{y^2}{2}=1$
- (b) a focus of the hyperbola is (2, 0)
- (c) the eccentricity of the hyperbola is
- (d) the equation of the hyperbola is ${x^2}-3y^2=3$
Hide Solution
Verified By Collegedunia
The Correct Option is D
Solution and Explanation
Here, equation of ellipse is$\frac{x^2}{4}+\frac{y^2}{1}=1$
$\Rightarrow$ $e^2=1-\frac{b^2}{a^2}=1-\frac{1}{4}=\frac{3}{4}$
$\therefore$ e$=\frac{\sqrt{3}}{2}$ and focus $(\pm \alpha e,0)\Rightarrow(\pm\sqrt{3},0)$
For hyperbola $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1,e^2_1=1+\frac{b^2}{a^2}$
where, $e^2_1=\frac{1}{e^2}=\frac{4}{3}\Rightarrow 1+\frac{b^2}{a^2}=\frac{4}{3}$
$\therefore$ $\frac{b^2}{a^2}=\frac{1}{3}$ ...........(i)
and hyperbola passes through $(\pm\sqrt{3},0)$
$\Rightarrow$ $\frac{3}{a^2}=1\Rightarrow \alpha^2=3$...........(ii)
From Eqs. (i) and (ii), $b^2-1$...................(iii)
$\therefore$ Equation of hyperbola is $\frac{x^2}{3}-{y^2}{1}=1$
Focus is $(\pm \alpha e_1,0)\Rightarrow \bigg(\pm\sqrt{3}.\frac{2}{\sqrt3,0}\bigg)\Rightarrow(\pm2,0)$
Hence, (b) and (d) are correct answers.
$\Rightarrow$ $e^2=1-\frac{b^2}{a^2}=1-\frac{1}{4}=\frac{3}{4}$
$\therefore$ e$=\frac{\sqrt{3}}{2}$ and focus $(\pm \alpha e,0)\Rightarrow(\pm\sqrt{3},0)$
For hyperbola $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1,e^2_1=1+\frac{b^2}{a^2}$
where, $e^2_1=\frac{1}{e^2}=\frac{4}{3}\Rightarrow 1+\frac{b^2}{a^2}=\frac{4}{3}$
$\therefore$ $\frac{b^2}{a^2}=\frac{1}{3}$ ...........(i)
and hyperbola passes through $(\pm\sqrt{3},0)$
$\Rightarrow$ $\frac{3}{a^2}=1\Rightarrow \alpha^2=3$...........(ii)
From Eqs. (i) and (ii), $b^2-1$...................(iii)
$\therefore$ Equation of hyperbola is $\frac{x^2}{3}-{y^2}{1}=1$
Focus is $(\pm \alpha e_1,0)\Rightarrow \bigg(\pm\sqrt{3}.\frac{2}{\sqrt3,0}\bigg)\Rightarrow(\pm2,0)$
Hence, (b) and (d) are correct answers.
Was this answer helpful?
0
0
Top Questions on Conic sections
- The sum of squares of all possible values of $k$, for which the area of the region bounded by the parabolas \[2y^2 = kx \quad \text{and} \quad ky^2 = 2(y - x)\]is maximum, is equal to:
- JEE Main - 2024
- Mathematics
- Conic sections
- Let a conic \( C \) pass through the point \( (4, -2) \) and \( P(x, y), \, x \geq 3 \), be any point on \( C \). Let the slope of the line touching the conic \( C \) only at a single point \( P \) be half the slope of the line joining the points \( P \) and \( (3, -5) \). If the focal distance of the point \( (7, 1) \) on \( C \) is \( d \), then \( 12d \) equals ______.
- JEE Main - 2024
- Mathematics
- Conic sections
- Let \(S\) be the focus of the hyperbola \(\frac{x^2}{3} - \frac{y^2}{5} = 1\), on the positive x-axis. Let \(C\) be the circle with its centre at \(A\left(\sqrt{6}, \sqrt{5}\right)\) and passing through the point \(S\). If \(O\) is the origin and \(SAB\) is a diameter of \(C\), then the square of the area of the triangle \(OSB\) is equal to -
- JEE Main - 2024
- Mathematics
- Conic sections
- The parabola \( y^2 = 4x \) divides the area of the circle \( x^2 + y^2 = 5 \) in two parts. The area of the smaller part is equal to:
- JEE Main - 2024
- Mathematics
- Conic sections
- Let \( A, B, \) and \( C \) be three points on the parabola \( y^2 = 6x \), and let the line segment \( AB \) meet the line \( L \) through \( C \) parallel to the \( x \)-axis at the point \( D \). Let \( M \) and \( N \) respectively be the feet of the perpendiculars from \( A \) and \( B \) on \( L \). Then \[ \left( \frac{\text{AM} \cdot \text{BN}}{\text{CD}} \right)^2 \] is equal to ______ .
- JEE Main - 2024
- Mathematics
- Conic sections
View More Questions
Questions Asked in JEE Advanced exam
- A closed vessel contains 10 g of an ideal gas X at 300 K, which exerts 2 atm pressure. At the same temperature, 80 g of another ideal gas Y is added to it and the pressure becomes 6 atm. The ratio of root mean square velocities of X and Y at 300 K is
- JEE Advanced - 2024
- States of matter
- Let the function \(f:[1,\infin)→\R\) be defined by
\(f(t) = \begin{cases} (-1)^{n+1}2, & \text{if } t=2n-1,n\in\N, \\ \frac{(2n+1-t)}{2}f(2n-1)+\frac{(t-(2n-1))}{2}f(2n+1) & \text{if } 2n-1<t<2n+1,n\in\N. \end{cases}\)
Define \(g(x)=\int\limits_{1}^{x}f(t)dt,x\in(1,\infin).\) Let α denote the number of solutions of the equation g(x) = 0 in the interval (1, 8] and \(β=\lim\limits_{x→1+}\frac{g(x)}{x-1}\). Then the value of α + β is equal to _____.- JEE Advanced - 2024
- Integral Calculus
- A dimensionless quantity is constructed in terms of electronic charge \(e\), permittivity of free space \(\epsilon_0\) , Planck’s constant ℎ, and speed of light c. If the dimensionless quantity is written as \(e^\alpha\epsilon_0^\beta h^\gamma c^\delta\)and n is a non-zero integer, then\((\alpha, \beta,\gamma,\delta)\) is given by
- JEE Advanced - 2024
- Semiconductor electronics: materials, devices and simple circuits
- A block of mass \(5 kg\) moves along the \(x-\)direction subject to the force \(F = (−20x + 10) N,\) with the value of \(x \) in metre. At time \(t = 0 s,\) it is at rest at position \(x = 1 m\). The position and momentum of the block at \(t = (\pi/4)\) s are
- JEE Advanced - 2024
- Work-energy theorem
- A region in the form of an equilateral triangle (in x-y plane) of height L has a uniform magnetic field 𝐵⃗ pointing in the +z-direction. A conducting loop PQR, in the form of an equilateral triangle of the same height 𝐿, is placed in the x-y plane with its vertex P at x = 0 in the orientation shown in the figure. At 𝑡 = 0, the loop starts entering the region of the magnetic field with a uniform velocity 𝑣 along the +x-direction. The plane of the loop and its orientation remain unchanged throughout its motion.
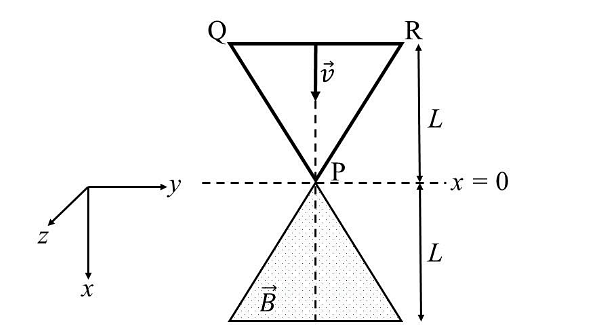
Which of the following graph best depicts the variation of the induced emf (E) in the loop as a function of the distance (𝑥) starting from 𝑥 = 0?
View More Questions



