Question:
Let R2 denote R × R. Let
S = {(a, b, c) : a, b, c ∈ R and ax2 + 2bxy + cy2 > 0 for all (x, y) ∈ R2 - {(0, 0}}.
Then which of the following statements is (are) TRUE ?
Let R2 denote R × R. Let
S = {(a, b, c) : a, b, c ∈ R and ax2 + 2bxy + cy2 > 0 for all (x, y) ∈ R2 - {(0, 0}}.
Then which of the following statements is (are) TRUE ?
S = {(a, b, c) : a, b, c ∈ R and ax2 + 2bxy + cy2 > 0 for all (x, y) ∈ R2 - {(0, 0}}.
Then which of the following statements is (are) TRUE ?
Updated On: Oct 24, 2024
- \((2,\frac{7}{2},6)\in S\)
- If \((3,b,\frac{1}{12})\in S\), then |2b| < 1.
- For any given (a, b, c) ∈ S, the system of linear equations
ax + by = 1
bx + cy = -1
has a unique solution. - For any given (a, b, c) ∈ S, the system of linear equations
(a + 1)x + by = 0
bx + (c + 1)y = 0
has a unique solution.
Hide Solution
Verified By Collegedunia
The Correct Option is B, C, D
Solution and Explanation
The correct option is (B): If \((3,b,\frac{1}{12})\in S\), then |2b| < 1., (C): For any given (a, b, c) ∈ S, the system of linear equations
ax + by = 1
bx + cy = -1
has a unique solution. and (D): For any given (a, b, c) ∈ S, the system of linear equations
(a + 1)x + by = 0
bx + (c + 1)y = 0
has a unique solution.
ax + by = 1
bx + cy = -1
has a unique solution. and (D): For any given (a, b, c) ∈ S, the system of linear equations
(a + 1)x + by = 0
bx + (c + 1)y = 0
has a unique solution.
Was this answer helpful?
0
3
Top Questions on Quadratic Equations
- The ratio of the sum and product of the roots of the quadratic equation \(7x^2-12x+18=0\) is
- AP POLYCET - 2024
- Mathematics
- Quadratic Equations
- If \(2\) is a root of the equation \(x^2-px+q=0\) and \(p^2=4q\), then the other root is
- AP POLYCET - 2024
- Mathematics
- Quadratic Equations
- Given \(x^2 - 70x + \lambda = 0\) with positive integral roots a and B where one of the root is less than 10, and \( \frac{\lambda}2 \times i \frac{\lambda}3\) are not integers, then find value of \(\frac{\sqrt{α-1} +\sqrt{β-1}}{|α-β|}\)
- JEE Main - 2024
- Mathematics
- Quadratic Equations
- The sum of roots of |x2 - 8x + 15| - 2x + 7 = 0 is:
- JEE Main - 2023
- Mathematics
- Quadratic Equations
- Let a and b are roots of x2 – 7x – 1 = 0. The value of \(\frac{a^{21} + b^{21} + a^{17} + b^{17}}{a^{19} + b^{19}}\) is?
- JEE Main - 2023
- Mathematics
- Quadratic Equations
View More Questions
Questions Asked in JEE Advanced exam
- A region in the form of an equilateral triangle (in x-y plane) of height L has a uniform magnetic field 𝐵⃗ pointing in the +z-direction. A conducting loop PQR, in the form of an equilateral triangle of the same height 𝐿, is placed in the x-y plane with its vertex P at x = 0 in the orientation shown in the figure. At 𝑡 = 0, the loop starts entering the region of the magnetic field with a uniform velocity 𝑣 along the +x-direction. The plane of the loop and its orientation remain unchanged throughout its motion.
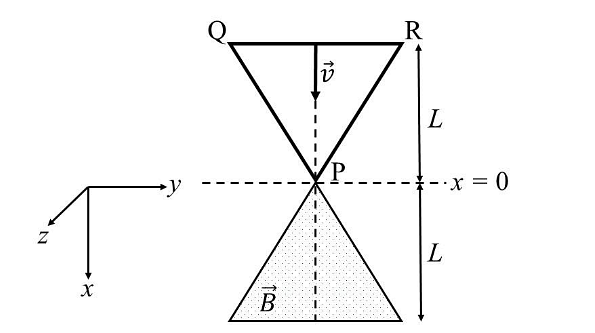
Which of the following graph best depicts the variation of the induced emf (E) in the loop as a function of the distance (𝑥) starting from 𝑥 = 0? - Two beads, each with charge q and mass m, are on a horizontal, frictionless, non-conducting, circular hoop of radius R. One of the beads is glued to the hoop at some point, while the other one performs small oscillations about its equilibrium position along the hoop. The square of the angular frequency of the small oscillations is given by [ \(\epsilon_0 \)is the permittivity of free space.]
- JEE Advanced - 2024
- Moving charges and magnetism
- A group of 9 students, s1, s2,…., s9, is to be divided to form three teams X, Y and Z of sizes 2, 3, and 4, respectively. Suppose that s1 cannot be selected for the team X and s2 cannot be selected for the team Y. Then the number of ways to form such teams, is _______.
- JEE Advanced - 2024
- Combinations
- Let \(\vec{p}=2\hat{i}+\hat{j}+3\hat{k}\) and \(\vec{q}=\hat{i}-\hat{j}+\hat{k}\). If for some real numbers α, β and γ we have
\(15\hat{i}+10\hat{j}+6\hat{k}=α(2\vec{p}+\vec{q})+β(\vec{p}-2\vec{q})+γ(\vec{p}\times\vec{q})\),
then the value of γ is ________.- JEE Advanced - 2024
- Vector Algebra
- Let X be a random variable, and let P(X = x) denote the probability that X takes the value x. Suppose that the points (x, P(X = x)), x = 0,1,2,3,4, lie on a fixed straight line in the xy -plane, and P(X = x) = 0 for all x ∈ R - {0,1,2,3,4}. If the mean of X is \(\frac{5}{2}\) , and the variance of X is α, then the value of 24α is ______.
- JEE Advanced - 2024
- Probability
View More Questions



