Let $d_1$ and $d_2$ be the lengths of the perpendiculars drawn from any point of the line $7x - 9y + 10 = 0$ upon the lines $3x + 4y = 5$ and $12x + 5y = 7$ respectively. Then
- $d_1 > d_2$
- $d_1 = d_2$
- $d_1 < d_2$
- $d_1 = 2d_2$
The Correct Option is B
Solution and Explanation
then $7 h-9 k+10=0$
$\Rightarrow 7 h =9 k-10$
$\Rightarrow h =\frac{9 k-10}{7}$ ... (i)
Now, perpendicular distance from point $(h, k)$
to the line $3 x+4 y=5$ is $d_{1}$
$ d_{1}=\frac{3 h+4 k-5}{\sqrt{3^{2}+4^{2}}} $
$\Rightarrow d_{1}=\frac{3 h+4 k-5}{5}$
$\Rightarrow d_{1}=\frac{3 h+4 k-5}{5}$ ... (ii)
and perpendicular distance from $(h, k)$ to the line $12 x+5 y=7$ is $d_{2}$
$\therefore d_{2}=\frac{12 h+5 k-7}{\sqrt{12^{2}+5^{2}}} $
$\Rightarrow d_{2}=\frac{12 h+5 k-7}{13}$ ... (iii)
Now, $d_{1}-d_{2}=\frac{3 h+4 k-5}{5}-\frac{12 h+5 k-7}{13}$
$\Rightarrow d_{1}-d_{2}$
$=\frac{13(3 h+4 k-5)-5(12 h+5 k-7)}{65}$
$=\frac{39 h+52 k-65-60 h-25 k+35}{65}$
$=\frac{-21 h+27 k-30}{65}$
$=\frac{-21\left(\frac{9 k-10}{7}\right)+27 k-30}{65} $
$=\frac{-27 k+30+27 k-30}{65}=0$ [fromE(i)]
$\Rightarrow d_{1}-d_{2}=0 $
$\Rightarrow d_{1}=d_{2}$
Top Questions on Straight lines
- A rectangle ABCD has its side parallel to the line y=2x and vertices A,B,D are on y=1,x=1 and x=-1 respectively. The coordinate of C can be
- WBJEE - 2023
- Mathematics
- Straight lines
- Let $S_1$ and $S_2$ be respectively the sets of all $a \in R -\{0\}$ for which the system of linear equations $ a x+2 a y-3 a z=1$ $ (2 a+1) x+(2 a+3) y+(a+1) z=2$ $(3 a+5) x+(a+5) y+(a+2) z=3$ has unique solution and infinitely many solutions Then
- JEE Main - 2023
- Mathematics
- Straight lines
- Orthocentre of triangle having vertices as A (1,2), B(3,-4), C(0,6) is
- JEE Main - 2023
- Mathematics
- Straight lines
- A rectangle is drawn by lines x=0, x=2, y=0 and y=5. Points A and B lie on coordinate axes. If line AB divides the area of rectangle in 4:1, then the locus of mid-point of AB is?
- JEE Main - 2023
- Mathematics
- Straight lines
- Let the six numbers $a_1, a_2, a_3, a_4, a_5, a_6$, be in AP and $a_1+a_3=10$ If the mean of these six numbers is $\frac{19}{2}$ and their variance is $\sigma^2$, then $8 \sigma^2$ is equal to :
- JEE Main - 2023
- Mathematics
- Straight lines
Questions Asked in WBJEE exam
- A train is moving along the tracks at a constant speed u. A girl on the train throws a ball of mass m straight ahead along the direction of motion of the train with speed v with respect to herself. Then,
- WBJEE - 2023
- Motion in a plane
- \(\lim_{x\rightarrow \infty}\){\(x-\sqrt[n]{(x-a_1)(x-a_2)......(x-a_n)}\)} where a1,a2,.....an are positive rational numbers.The limit
- A body of mass 2 kg moves in a horizontal circular path of radius 5m. In an instant its speed is \(2\sqrt5\) m/s and is increasing at the rate of 3 m/s2.The magnitude of the force acting on the body at the instant is,
- WBJEE - 2023
- Motion in a plane
- If z1 and z2 are two complex numbers satisfying the equation\(|\frac{z_1+z_2}{z_1-z_2}|=1\), then \(\frac{z_1}{z_2}\) may be
- WBJEE - 2023
- complex numbers
- A ray of monochromatic light is incident on the plane surface of separation between two media X and Y with the angle of incidence 'i' in medium X and angle of refraction 'r' in medium Y. The given graph shows the relation between sin i and sin r. If Vx and Vy are the velocities of the ray in media X and Y respectively, Then which of the following is true?
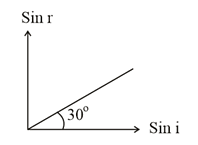
- WBJEE - 2023
- Ray optics and optical instruments
Concepts Used:
Straight lines
A straight line is a line having the shortest distance between two points.
A straight line can be represented as an equation in various forms, as show in the image below:

The following are the many forms of the equation of the line that are presented in straight line-
1. Slope – Point Form
Assume P0(x0, y0) is a fixed point on a non-vertical line L with m as its slope. If P (x, y) is an arbitrary point on L, then the point (x, y) lies on the line with slope m through the fixed point (x0, y0) if and only if its coordinates fulfil the equation below.
y – y0 = m (x – x0)
2. Two – Point Form
Let's look at the line. L crosses between two places. P1(x1, y1) and P2(x2, y2) are general points on L, while P (x, y) is a general point on L. As a result, the three points P1, P2, and P are collinear, and it becomes
The slope of P2P = The slope of P1P2 , i.e.
\(\frac{y-y_1}{x-x_1} = \frac{y_2-y_1}{x_2-x_1}\)
Hence, the equation becomes:
y - y1 =\( \frac{y_2-y_1}{x_2-x_1} (x-x1)\)
3. Slope-Intercept Form
Assume that a line L with slope m intersects the y-axis at a distance c from the origin, and that the distance c is referred to as the line L's y-intercept. As a result, the coordinates of the spot on the y-axis where the line intersects are (0, c). As a result, the slope of the line L is m, and it passes through a fixed point (0, c). The equation of the line L thus obtained from the slope – point form is given by
y – c =m( x - 0 )
As a result, the point (x, y) on the line with slope m and y-intercept c lies on the line, if and only if
y = m x +c



