Question:
In the given circuit, the AC source has ? = 100 rad/s.
Considering the inductor and capacitor to be ideal, the
correct choice(s) is(are)
In the given circuit, the AC source has ? = 100 rad/s.
Considering the inductor and capacitor to be ideal, the
correct choice(s) is(are)
Updated On: Jun 14, 2022
- The current through the circuit, I is 0.3 A
- The current through the circuit, I is $0.3 \, \sqrt{2}A$
- The voltage across $100 \Omega$ resistor = $10 \sqrt{2}V$
- The voltage across $50 \Omega$ resistor = 10 V
Hide Solution
Verified By Collegedunia
The Correct Option is C
Solution and Explanation
Circuit 1
$\, \, \, \, \, \, \, \, \, X_c = \frac{1}{\omega C} = 100 \Omega$
$\therefore \, \, \, \, \, \, \, \, Z_1 = \sqrt{(100)^2 + (100)^2}$
$ \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, = 100 \sqrt{2} \, \Omega$
$ \, \, \, \, \, \, \, \, \, \, \, \, \, \phi_1 = cos^{-1} \bigg( \frac{R_1}{Z_1}\bigg) = 45^{\circ} $
In this circuit current leads the voltage.
$\, \, \, \, \, \, \, \, \, \, I_1 = \frac{V}{Z_1} = \frac{20}{100 \sqrt{2}} = \frac{1}{5 \sqrt{2}} A$
$\, \, \, \, \, \, \, \, \, V_{100 \Omega} = (100) I_1 = (100) \frac{1}{5 \sqrt{2}} V$
$ \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, = 10 \sqrt{2} V$
Circuit 2
$\, \, \, \, \, \, \, \, \, \, \, \, X_L = \omega L = (100)(0.5) = 50 \Omega $
$\, \, \, \, \, \, \, \, \, \, \, \, \, Z_2 = \sqrt{(50)^2 + (50)^2} = 50\sqrt{2} \Omega$
$ \, \, \, \, \, \, \, \, \, \, \, \, \, \phi_1 = cos^{-1} \bigg( \frac{R_1}{Z_1}\bigg) = 45^{\circ} $
In this circuit voltage leads the current.
$\, \, \, \, \, \, \, \, \, \, I_2 = \frac{V}{Z_2} = \frac{20}{50 \sqrt{2}} = \frac{\sqrt{2}}{5} A$
$\, \, \, \, \, \, \, \, \, V_{50 \Omega} = (50) I_2 = 50 \bigg( \frac{ \sqrt{2}}{5}\bigg) = 10\sqrt{2} V$
Further, $I_1$ and $I_2$ have a mutual phase difference of $90^{\circ}$
$I = \sqrt{I^2 , + I^2_2} = 0.34$
$\, \, \, \, \, \, \, \, \, X_c = \frac{1}{\omega C} = 100 \Omega$
$\therefore \, \, \, \, \, \, \, \, Z_1 = \sqrt{(100)^2 + (100)^2}$
$ \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, = 100 \sqrt{2} \, \Omega$
$ \, \, \, \, \, \, \, \, \, \, \, \, \, \phi_1 = cos^{-1} \bigg( \frac{R_1}{Z_1}\bigg) = 45^{\circ} $
In this circuit current leads the voltage.
$\, \, \, \, \, \, \, \, \, \, I_1 = \frac{V}{Z_1} = \frac{20}{100 \sqrt{2}} = \frac{1}{5 \sqrt{2}} A$
$\, \, \, \, \, \, \, \, \, V_{100 \Omega} = (100) I_1 = (100) \frac{1}{5 \sqrt{2}} V$
$ \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, = 10 \sqrt{2} V$
Circuit 2
$\, \, \, \, \, \, \, \, \, \, \, \, X_L = \omega L = (100)(0.5) = 50 \Omega $
$\, \, \, \, \, \, \, \, \, \, \, \, \, Z_2 = \sqrt{(50)^2 + (50)^2} = 50\sqrt{2} \Omega$
$ \, \, \, \, \, \, \, \, \, \, \, \, \, \phi_1 = cos^{-1} \bigg( \frac{R_1}{Z_1}\bigg) = 45^{\circ} $
In this circuit voltage leads the current.
$\, \, \, \, \, \, \, \, \, \, I_2 = \frac{V}{Z_2} = \frac{20}{50 \sqrt{2}} = \frac{\sqrt{2}}{5} A$
$\, \, \, \, \, \, \, \, \, V_{50 \Omega} = (50) I_2 = 50 \bigg( \frac{ \sqrt{2}}{5}\bigg) = 10\sqrt{2} V$
Further, $I_1$ and $I_2$ have a mutual phase difference of $90^{\circ}$
$I = \sqrt{I^2 , + I^2_2} = 0.34$
Was this answer helpful?
0
0
Top Questions on LCR Circuit
- A logic circuit provides the output y as per the following truth table:
A B Y 0 0 1 0 1 0 1 0 1 1 1 0
The expression for the output Y is:- NEET (UG) - 2024
- Physics
- LCR Circuit
- Output of given circuit represents which logic gate :

- JEE Main - 2024
- Physics
- LCR Circuit
- Total impedance of a series LCR circuit varies with angular frequency of the AC source connected to it as shown in the graph. The quality factor Q of the series LCR circuit is

- KCET - 2023
- Physics
- LCR Circuit
- A series LCR circuit is connected to an $AC$ source of $220 V , 50 Hz$ The circuit contains a resistance $R =80 \Omega$, an inductor of inductive reactance $X _{ L }=70 \Omega$, and a capacitor of capacitive reactance $X _{ C }=130 \Omega$ The power factor of circuit is $\frac{x}{10}$ The value of $x$ is :
- JEE Main - 2023
- Physics
- LCR Circuit
- Figure shows a part of an electric circuit. The potentials at the points a, b and c are 30V, 12V and 2V respectively. the currents through the 20 resistors will be.

- JEE Main - 2023
- Physics
- LCR Circuit
View More Questions
Questions Asked in JEE Advanced exam
- A region in the form of an equilateral triangle (in x-y plane) of height L has a uniform magnetic field 𝐵⃗ pointing in the +z-direction. A conducting loop PQR, in the form of an equilateral triangle of the same height 𝐿, is placed in the x-y plane with its vertex P at x = 0 in the orientation shown in the figure. At 𝑡 = 0, the loop starts entering the region of the magnetic field with a uniform velocity 𝑣 along the +x-direction. The plane of the loop and its orientation remain unchanged throughout its motion.
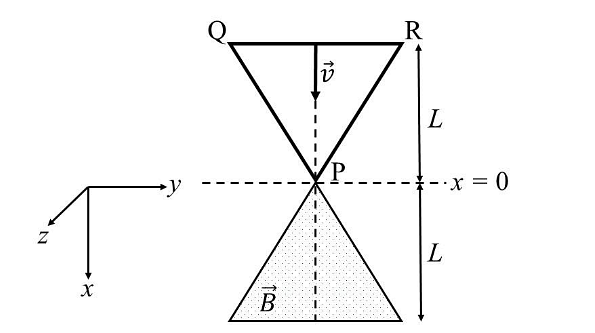
Which of the following graph best depicts the variation of the induced emf (E) in the loop as a function of the distance (𝑥) starting from 𝑥 = 0? - Two beads, each with charge q and mass m, are on a horizontal, frictionless, non-conducting, circular hoop of radius R. One of the beads is glued to the hoop at some point, while the other one performs small oscillations about its equilibrium position along the hoop. The square of the angular frequency of the small oscillations is given by [ \(\epsilon_0 \)is the permittivity of free space.]
- JEE Advanced - 2024
- Moving charges and magnetism
- A group of 9 students, s1, s2,…., s9, is to be divided to form three teams X, Y and Z of sizes 2, 3, and 4, respectively. Suppose that s1 cannot be selected for the team X and s2 cannot be selected for the team Y. Then the number of ways to form such teams, is _______.
- JEE Advanced - 2024
- Combinations
- Let \(\vec{p}=2\hat{i}+\hat{j}+3\hat{k}\) and \(\vec{q}=\hat{i}-\hat{j}+\hat{k}\). If for some real numbers α, β and γ we have
\(15\hat{i}+10\hat{j}+6\hat{k}=α(2\vec{p}+\vec{q})+β(\vec{p}-2\vec{q})+γ(\vec{p}\times\vec{q})\),
then the value of γ is ________.- JEE Advanced - 2024
- Vector Algebra
- Let X be a random variable, and let P(X = x) denote the probability that X takes the value x. Suppose that the points (x, P(X = x)), x = 0,1,2,3,4, lie on a fixed straight line in the xy -plane, and P(X = x) = 0 for all x ∈ R - {0,1,2,3,4}. If the mean of X is \(\frac{5}{2}\) , and the variance of X is α, then the value of 24α is ______.
- JEE Advanced - 2024
- Probability
View More Questions
Concepts Used:
LCR Circuit
An LCR circuit, also known as a resonant circuit, or an RLC circuit, is an electrical circuit consist of an inductor (L), capacitor (C) and resistor (R) connected in series or parallel.

Series LCR circuit
When a constant voltage source is connected across a resistor a current is induced in it. This current has a unique direction and flows from the negative to positive terminal. Magnitude of current remains constant.
Alternating current is the current if the direction of current through this resistor changes periodically. An AC generator or AC dynamo can be used as AC voltage source.




