Question:
In the figure, a ladder of mass $m$ is shown leaning against a wall. It is in static equilibrium making an angle $\theta$ with the horizontal floor. The coefficient of friction between the wall and the ladder is $\mu_{1}$ and that between the floor and the ladder is $\mu_{2}$. The normal reaction of the wall on the ladder is $N _{1}$ and that of the floor is $N _{2}$. If the ladder is about to slip, then
In the figure, a ladder of mass $m$ is shown leaning against a wall. It is in static equilibrium making an angle $\theta$ with the horizontal floor. The coefficient of friction between the wall and the ladder is $\mu_{1}$ and that between the floor and the ladder is $\mu_{2}$. The normal reaction of the wall on the ladder is $N _{1}$ and that of the floor is $N _{2}$. If the ladder is about to slip, then
Updated On: Jun 14, 2022
- $\mu_1=0, \mu_2 \ne 0$ and $N_2 \tan\theta=\frac{mg}{2}$
- $\mu_1\ne 0, \mu_2 = 0$ and $N_1 \tan \theta=\frac{mg}{2}$
- $\mu_1\ne 0, \mu_2 \ne 0$ and $N_2 =\frac{mg}{1+\mu_1\mu_2}$
- $\mu_1=0, \mu_2 \ne 0$ and $N_1 \tan \theta=\frac{mg}{2}$
Hide Solution
Verified By Collegedunia
The Correct Option is D
Solution and Explanation
Condition of translational equilibrium
$N _{1}=\mu_{2} \,N _{2} $
$N _{2}+\mu_{1}\, N _{1}= Mg$
Solving $N _{2}=\frac{ mg }{1+\mu_{1} \mu_{2}}$
$N _{1}=\frac{\mu_{2} mg }{1+\mu_{1} \mu_{2}}$
Applying torque equation about corner (left) point on the floor
$mg \frac{\ell}{2} \cos \theta= N _{1} \ell \sin \theta+\mu_{1} N _{1} \ell \cos \theta$
Solving $\tan \theta=\frac{1-\mu_{1} \mu_{2}}{2 \mu_{2}}$
$N _{1}=\mu_{2} \,N _{2} $
$N _{2}+\mu_{1}\, N _{1}= Mg$
Solving $N _{2}=\frac{ mg }{1+\mu_{1} \mu_{2}}$
$N _{1}=\frac{\mu_{2} mg }{1+\mu_{1} \mu_{2}}$
Applying torque equation about corner (left) point on the floor
$mg \frac{\ell}{2} \cos \theta= N _{1} \ell \sin \theta+\mu_{1} N _{1} \ell \cos \theta$
Solving $\tan \theta=\frac{1-\mu_{1} \mu_{2}}{2 \mu_{2}}$
Was this answer helpful?
0
0
Top Questions on System of Particles & Rotational Motion
- A particle moves in a straight line so that its displacement $x$ at any time $t$ is given by $x^2 = 1 + t^2$.
Its acceleration at any time $t$ is $x^{-n}$ where $n =$ ____.- JEE Main - 2024
- Physics
- System of Particles & Rotational Motion
- A particle is moving in circular path of radius r speed v such that speed is proportional to radius as \(V∝ r^{\frac{3}{2}}\). Then how does time period of revolution depends on r i.e Trn then \(n\) is.
- JEE Main - 2024
- Physics
- System of Particles & Rotational Motion
- A particle of mass m is projected at velocity at a velocity u, making an angle θ with the horizontal(x-axis). If the angle of projection θ is varied keeping all other parameters same, then magnitude of angular momentum(L) at its maximum height about the point of projection varies with θ as,
- WBJEE - 2023
- Physics
- System of Particles & Rotational Motion
- The ratio of radius of gyration of a solid sphere of mass M and radius R about its own axis to the radius of gyration of the thin hollow sphere of same mass and radius about its axis is:
- NEET (UG) - 2023
- Physics
- System of Particles & Rotational Motion
- A charged particle is subjected to acceleration in a cyclotron as shown. The charged particle undergoes increase in its speed

- KCET - 2023
- Physics
- System of Particles & Rotational Motion
View More Questions
Questions Asked in JEE Advanced exam
- A closed vessel contains 10 g of an ideal gas X at 300 K, which exerts 2 atm pressure. At the same temperature, 80 g of another ideal gas Y is added to it and the pressure becomes 6 atm. The ratio of root mean square velocities of X and Y at 300 K is
- JEE Advanced - 2024
- States of matter
- Let the function \(f:[1,\infin)→\R\) be defined by
\(f(t) = \begin{cases} (-1)^{n+1}2, & \text{if } t=2n-1,n\in\N, \\ \frac{(2n+1-t)}{2}f(2n-1)+\frac{(t-(2n-1))}{2}f(2n+1) & \text{if } 2n-1<t<2n+1,n\in\N. \end{cases}\)
Define \(g(x)=\int\limits_{1}^{x}f(t)dt,x\in(1,\infin).\) Let α denote the number of solutions of the equation g(x) = 0 in the interval (1, 8] and \(β=\lim\limits_{x→1+}\frac{g(x)}{x-1}\). Then the value of α + β is equal to _____.- JEE Advanced - 2024
- Integral Calculus
- A dimensionless quantity is constructed in terms of electronic charge \(e\), permittivity of free space \(\epsilon_0\) , Planck’s constant ℎ, and speed of light c. If the dimensionless quantity is written as \(e^\alpha\epsilon_0^\beta h^\gamma c^\delta\)and n is a non-zero integer, then\((\alpha, \beta,\gamma,\delta)\) is given by
- JEE Advanced - 2024
- Semiconductor electronics: materials, devices and simple circuits
- A block of mass \(5 kg\) moves along the \(x-\)direction subject to the force \(F = (−20x + 10) N,\) with the value of \(x \) in metre. At time \(t = 0 s,\) it is at rest at position \(x = 1 m\). The position and momentum of the block at \(t = (\pi/4)\) s are
- JEE Advanced - 2024
- Work-energy theorem
- A region in the form of an equilateral triangle (in x-y plane) of height L has a uniform magnetic field 𝐵⃗ pointing in the +z-direction. A conducting loop PQR, in the form of an equilateral triangle of the same height 𝐿, is placed in the x-y plane with its vertex P at x = 0 in the orientation shown in the figure. At 𝑡 = 0, the loop starts entering the region of the magnetic field with a uniform velocity 𝑣 along the +x-direction. The plane of the loop and its orientation remain unchanged throughout its motion.
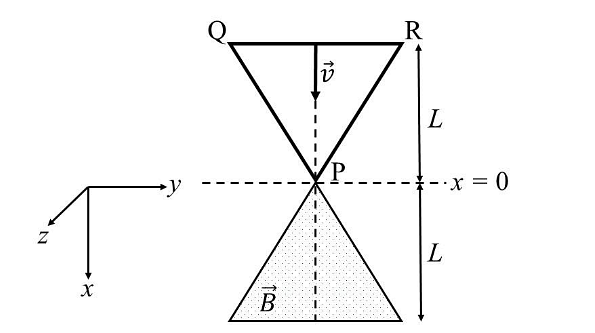
Which of the following graph best depicts the variation of the induced emf (E) in the loop as a function of the distance (𝑥) starting from 𝑥 = 0?
View More Questions
Concepts Used:
System of Particles and Rotational Motion
- The system of particles refers to the extended body which is considered a rigid body most of the time for simple or easy understanding. A rigid body is a body with a perfectly definite and unchangeable shape.
- The distance between the pair of particles in such a body does not replace or alter. Rotational motion can be described as the motion of a rigid body originates in such a manner that all of its particles move in a circle about an axis with a common angular velocity.
- The few common examples of rotational motion are the motion of the blade of a windmill and periodic motion.



