Question

If $ABCD$ is a cyclic quadrilateral with $AB = 6, BC = 4, CD = 5, DA = 3$ and $\angle ABC$ = $\theta$ then $cos\, \theta$ =

• A. $\frac{3}{13}$
• B. $\frac{18}{76}$
• C. $\frac{16}{78}$
• D. $\frac{78}{86}$

Answer 1

The Correct Option is A

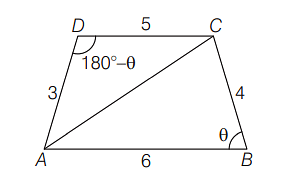
In $\Delta A B C$,
$A C^{2}=A B^{2}+B C^{2}-2(A B)(A C) \cos \theta[$ By Cosine rule $]$
$\Rightarrow A C^{2}=6^{2}+4^{2}-2(6)(4) \cos \theta$
$\Rightarrow A C^{2}=36+16-48 \cos \theta $
$\Rightarrow A C^{2}=52-48 \cos \theta \dots$(i)
Now, In $\Delta A D C$
$A C^{2}=A D^{2}+D C^{2}-2(A D)(D C) \cos \left(180^{\circ}-\theta\right)$
$=3^{2}+5^{2}+2(3)(5) \cos \theta [$ By Cosine rule $]$
$A C^{2}=9+25+30 \cos \theta $
$A C^{2}=34+30 \cos \theta \dots$(ii)
By Eqs. (i) and (ii), we get
$52-48 \cos \theta=34+30 \cos \theta$
$\Rightarrow 52-34=48 \cos \theta+30 \cos \theta $
$ \Rightarrow 18=78 \cos \theta $
$ \Rightarrow \cos \theta=\frac{18}{78}=\frac{3}{13}$