If $k$ is one of the roots of the equation $x^2 - 25x + 24 = 0 $ such that $A = \begin{bmatrix}1&2&1\\ 3&2&3\\ 1&1&k\end{bmatrix} $ is a non-singular matrix, then $A^{-1}$ =
- $- \frac{1}{46} \begin{bmatrix}90&-94&8\\ -138&46&0\\ 2&2&-8\end{bmatrix} $
- $- \frac{1}{92} \begin{bmatrix}45&-47&4\\ -69&23&0\\ 1&1&4\end{bmatrix} $
- $ - \frac{1}{46} \begin{bmatrix}45&-47&4\\ -69&23&0\\ 1&1&-4\end{bmatrix} $
- $ - \frac{1}{92} \begin{bmatrix}90&-94&8\\ -138&46&0\\ 2&2&-8\end{bmatrix} $
The Correct Option is B
Solution and Explanation
$ x^{2}-x-24 x+24 = 0 $
$= x(x-1)-24(x-1)= 0 $
$= (x-1)(x-24) =0$
$ \Rightarrow x=1,24$
$\because k$ is one of the root of the E (i),
$\therefore k=1, 24$
If $k = 1$,
$\therefore A= \begin{bmatrix} 1 & 2 & 1 \\ 3 & 2 & 3 \\ 1 & 1 & 1\end{bmatrix}$
$|A| =1(2-3)-2(3-3)+1(3-2) $
$=-1-0+1=0 $
$|A| =0 $
$k=1$, not possible, because given matrix $A$ is singular.
Now, $k=24$,
$ \therefore A =\begin{bmatrix} 1 & 2 & 1 \\ 3 & 2 & 3 \\ 1 & 1 & 24\end{bmatrix} $
$ |A| =1(48-3)-2(72-3)+1(3-2) $
$=45-138+1=-92 \neq 0 $
adj $A =\begin{bmatrix} 45 & -69 & 1 \\ -47 & 23 & 1 \\ 4 & 0 & -4\end{bmatrix}^{1}$ $=\begin{bmatrix}45 & -47 & 4 \\ -69 & 23 & 0 \\ 1 & 1 & -4\end{bmatrix}$
$ A^{-1} =\frac{1}{|A|} \cdot \text{adj} A $
$=-\frac{1}{92}\begin{bmatrix}45 & -47 & 4 \\ -69 & 23 & 0 \\ 1 & 1 & -4\end{bmatrix} $
Top Questions on Transpose of a Matrix
- Let P be a square matrix such that P2 = I – P. For α, β, γ, δ ∈ N, if Pα + Pβ = γI – 29P and Pα – Pβ = δI – 13P, then α + β + γ – δ is equal to
- JEE Main - 2023
- Mathematics
- Transpose of a Matrix
- Let B =\(\begin{bmatrix} 1 & 3 & α \\ 1 & 2& 3 \\ α & α & 4 \end{bmatrix}\) , α>2 be the adjoint of a matrix A and |A| = 2, then [α - 2α α] B\(\begin{bmatrix} α \\ -2α \\ α \end{bmatrix}\)is equal to
- JEE Main - 2023
- Mathematics
- Transpose of a Matrix
- Given below are two statements: one is labelled as Assertion A and the other is labelled as Reason R.
Assertion A : For matrix A =\(\begin{bmatrix} 1 & 2 \\ 8 & 16 \end{bmatrix}\),rank of A = r(A) = 1
Reason R: For matrix A if |A| = 0, then it implies that rank of matrix A given by r(A) is less than full rank.
In the light of the above statements, choose the most appropriate answer from the options given below:- CUET (PG) - 2023
- Mathematics
- Transpose of a Matrix
- if A=\(\frac{1}{5! 6! 7!}\begin{bmatrix} 5! & 6! & 7!\\ 6! & 7! & 8! \\ 7! & 8! & 9! \end{bmatrix}\), then |adj(adj(2A))| is equal t
- JEE Main - 2023
- Mathematics
- Transpose of a Matrix
- Let Dk=\(\begin{vmatrix} 1 & 2k & 2k-1\\ n & n^2+n+2 & n^2 \\ n & n^2+n & n^2+n+2 \end{vmatrix} \) If \(∑^n_{k=1} D_k=96,\) The n is equal to
- JEE Main - 2023
- Mathematics
- Transpose of a Matrix
Questions Asked in AP EAMCET exam
Six coins tossed simultaneously then find the probability of getting at least 4 heads.
- AP EAMCET - 2023
- Probability
- In the chessboard if the rectangle form is 1296, find the total number of squares formed.
- AP EAMCET - 2023
- Coordinate Geometry
Find the products formed if chlorine reacts with the cold and dilute sodium hydroxide solution.
- AP EAMCET - 2023
- Chemical Reactions
- Find the coefficient of \(\frac{y^3}{x^8}\) in \((x+y)^{-5}\) ?
- AP EAMCET - 2023
- Binomial theorem
- Which compound is gem-dihalide?
- AP EAMCET - 2023
- Organic Chemistry- Some Basic Principles and Techniques
Concepts Used:
Transpose of a Matrix
The matrix acquired by interchanging the rows and columns of the parent matrix is called the Transpose matrix. The transpose matrix is also defined as - “A Matrix which is formed by transposing all the rows of a given matrix into columns and vice-versa.”
The transpose matrix of A is represented by A’. It can be better understood by the given example:

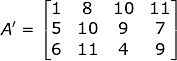
Now, in Matrix A, the number of rows was 4 and the number of columns was 3 but, on taking the transpose of A we acquired A’ having 3 rows and 4 columns. Consequently, the vertical Matrix gets converted into Horizontal Matrix.
Hence, we can say if the matrix before transposing was a vertical matrix, it will be transposed to a horizontal matrix and vice-versa.
Read More: Transpose of a Matrix



