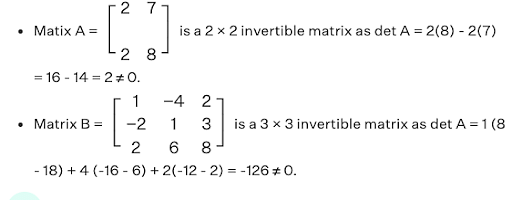Question:
If $A$ is a square matrix of order 3 , then | adj $\left(\operatorname{adj} A^{2}\right) \mid$ is equal to
If $A$ is a square matrix of order 3 , then | adj $\left(\operatorname{adj} A^{2}\right) \mid$ is equal to
Updated On: Aug 15, 2024
- $|A |^{2}$
- $|A|^{4}$
- $|A|^{8}$
- $|A|^{16}$
Hide Solution
Verified By Collegedunia
The Correct Option is C
Solution and Explanation
We know that,
$|\operatorname{adj}(\operatorname{adj} A)| =|A|^{(n-1)^{2}}$
$\left|\operatorname{adj}\left(\operatorname{adj} A^{2}\right)\right| =\left|A^{2}\right|^{(3-1)^{2}} $
$=\left|A^{2}\right|^{2} \,\,[\because n=3] $
$=\left|A^{2}\right|^{4}=|A|^{8}$
$|\operatorname{adj}(\operatorname{adj} A)| =|A|^{(n-1)^{2}}$
$\left|\operatorname{adj}\left(\operatorname{adj} A^{2}\right)\right| =\left|A^{2}\right|^{(3-1)^{2}} $
$=\left|A^{2}\right|^{2} \,\,[\because n=3] $
$=\left|A^{2}\right|^{4}=|A|^{8}$
Was this answer helpful?
0
0
Top Questions on Invertible Matrices
- If A is a non-identity invertible symmetric matrix, then \(A^{-1}\) is:
- CUET (UG) - 2023
- Mathematics
- Invertible Matrices
- The number of matrices of order 3 × 3, whose entries are either 0 or 1 and the sum of all the entries is a prime number, is _________.
- JEE Main - 2022
- Mathematics
- Invertible Matrices
- Which of the following matrices can NOT be obtained from the matrix \(\begin{bmatrix} -1 &2 \\ 1 & -1 \end{bmatrix}\) by a single elementary row operation?
- JEE Main - 2022
- Mathematics
- Invertible Matrices
- If A and B are invertible matrices then which of the following is not correct ?
- KCET - 2021
- Mathematics
- Invertible Matrices
- The inverse of the matrix $\begin{bmatrix}2&5&0\\ 0&1&1\\ -1&0&3\end{bmatrix} $ is
- KCET - 2019
- Mathematics
- Invertible Matrices
View More Questions
Questions Asked in EAMCET exam
- If $\quad \tan \theta \cdot \tan \left(120^{\circ}-\theta\right) \tan \left(120^{\circ}+\theta\right)=\frac{1}{\sqrt{3}}$, then $\theta$ is equal to
- EAMCET - 2015
- Trigonometric Equations
- If $f: R \rightarrow R, g: R \rightarrow R$ are defined by $f(x)=5\, x-3, g(x)=x^{2}+3$, then $g o f^{-1}(3)$ is equal to
- EAMCET - 2015
- Differentiability
- The common roots of the equations $z^{3}+2 z^{2}+2 z+1=0, z^{2014}+z^{2015}+1=0$ are
- EAMCET - 2015
- Quadratic Equations
- The value of the sum $1 \cdot 2 \cdot 3+2 \cdot 3 \cdot 4+3 \cdot 4 \cdot 5+\ldots$ upto $n$ terms is equal to
- EAMCET - 2015
- Sum of First n Terms of an AP
- The system $2\,x+3 y+z=5,3\,x+y+5\,z=7$ and $x+4\,y-2\,z=3$ has
- EAMCET - 2015
- Transpose of a Matrix
View More Questions
Concepts Used:
Invertible matrices
A matrix for which matrix inversion operation exists, given that it satisfies the requisite conditions is known as an invertible matrix. Any given square matrix A of order n × n is called invertible if and only if there exists, another n × n square matrix B such that, AB = BA = In, where In is an identity matrix of order n × n.
For example,
It can be observed that the determinant of the following matrices is non-zero.