An electric field \( \vec{E} = (2x \hat{i}) \, \text{N C}^{-1} \) exists in space. A cube of side \( 2 \, \text{m} \) is placed in the space as per the figure given below. The electric flux through the cube is __________ \( \text{N m}^2/\text{C} \).
Correct Answer: 16
Solution and Explanation
\documentclass{article} \usepackage[utf8]{inputenc} \usepackage{amsmath} \begin{document} The electric flux is given by Gauss's Law: \[ \Phi = \oint \vec{E} \cdot d\vec{A}. \] The field $\vec{E} = 2x \hat{i}$ varies with $x$. For the cube, only the left ($x = 0$) and right ($x = 2$) faces contribute: \[ \Phi = E_\text{right} A - E_\text{left} A. \] Substituting $A = 4 \, \mathrm{m}^2$, $E_\text{right} = 2(2) = 4$, and $E_\text{left} = 2(0) = 0$: \[ \Phi = 4 \cdot 4 - 0 \cdot 4 = 16 \, \mathrm{Nm}^2/\mathrm{C}. \]
Top Questions on Gauss Law
- There are two cubical Gaussian surface carrying charges as shown. Find ratio of fluxes through surface \(C_1\) and \(C_2\):

- JEE Main - 2024
- Physics
- Gauss Law
- A cubical Gaussian surface has side of length a = 10 cm. Electric field lines are parallel to x-axis as shown. The magnitudes of electric fields through surfaces ABCD and EFGH are 6kNC-1 and 9kNC-1 respectively. Then the total charge enclosed by the cube is
[Take ε0 = 9 × 10-12 Fm-1]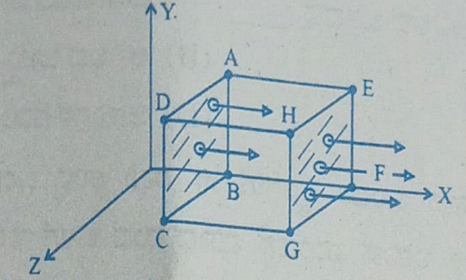
- KCET - 2023
- Physics
- Gauss Law
A cubical volume is bounded by the surfaces $x=0, x= a , y=0, y= a , z=0, z= a$ The electric field in the region is given by $\vec{E}=E_0 x \hat{ t }$ Where $E_0=4 \times 10^4 NC ^{-1} m ^{-1}$ If $a=2 cm$, the charge contained in the cubical volume is $Q \times 10^{-14} C$ The value of $Q$ is ___ Take \(E_{0}=9\times 10^{-2}C^{2}/Nm^{2}\)
- JEE Main - 2023
- Physics
- Gauss Law
- The electric potential at the center of two concentric half rings of radii $R_1$ and $R_2$, having same linear charge density $\lambda$ is :
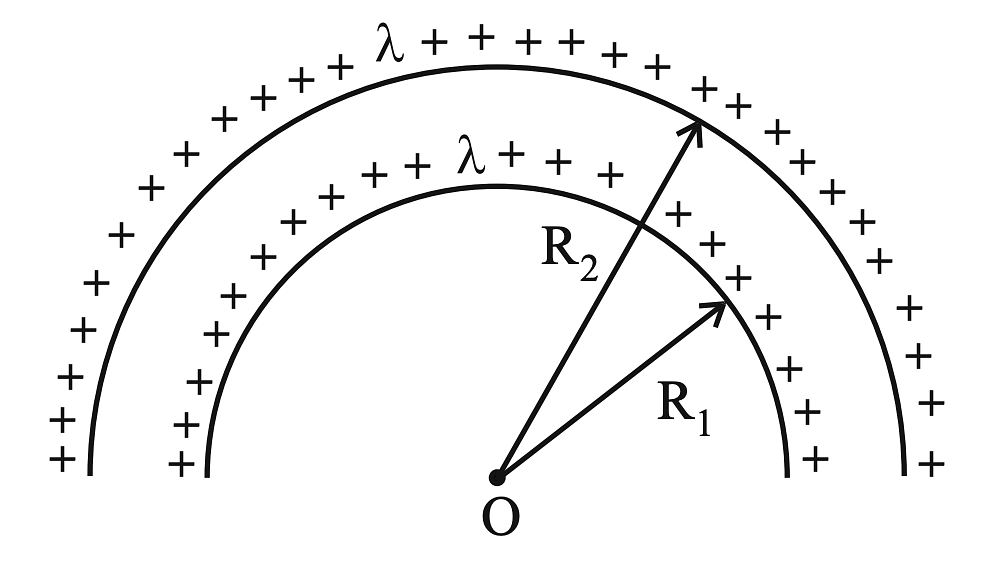
- JEE Main - 2023
- Physics
- Gauss Law
- Match List I with List IIChoose the correct answer from the options given below:
LIST I LIST II A Gauss's Law in Electrostatics I \(\oint \vec{E} \cdot d \vec{l}=-\frac{d \phi_B}{d t}\) B Faraday's Law II \(\oint \vec{B} \cdot d \vec{A}=0\) C Gauss's Law in Magnetism III \(\oint \vec{B} \cdot d \vec{l}=\mu_0 i_c+\mu_0 \in_0 \frac{d \phi_E}{d t}\) D Ampere-Maxwell Law IV \(\oint \vec{E} \cdot d \vec{s}=\frac{q}{\epsilon_0}\) - JEE Main - 2023
- Physics
- Gauss Law
Questions Asked in JEE Main exam

In the truth table of the above circuit the value of X and Y are- JEE Main - 2024
- Logic gates
- A spherical ball of radius \( 1 \times 10^{-4} \, \text{m} \) and density \( 10^5 \, \text{kg/m}^3 \) falls freely under gravity through a distance \( h \) before entering a tank of water. If after entering in water the velocity of the ball does not change, then the value of \( h \) is approximately: \[ \text{(The coefficient of viscosity of water is } 9.8 \times 10^{-6} \, \text{N s/m}^2 \text{)} \]
- JEE Main - 2024
- Gauss's, Green's and Stokes’ theorems
- At room temperature (\( 27^\circ\text{C} \)), the resistance of a heating element is \( 50 \, \Omega \). The temperature coefficient of the material is \( 2.4 \times 10^{-4} \, ^\circ\text{C}^{-1} \). The temperature of the element, when its resistance is \( 62 \, \Omega \), is _________\(\degree C\).
- JEE Main - 2024
- Thermodynamics
- A 1 kg mass is suspended from the ceiling by a rope of length 4m. A horizontal force 'F' is applied at the mid point of the rope so that the rope makes an angle of 45° with respect to the vertical axis as shown in figure. The magnitude of F is

- JEE Main - 2024
- Newtons Laws of Motion
- A real gas within a closed chamber at \( 27^\circ \text{C} \) undergoes the cyclic process as shown in the figure. The gas obeys \( PV^3 = RT \) equation for the path \( A \) to \( B \). The net work done in the complete cycle is (assuming \( R = 8 \, \text{J/mol K} \)):

- JEE Main - 2024
- Thermodynamics



