Question:
A thin stiff insulated metal wire is bent into a circular loop with its two ends extending tangentially from the same point of the loop. The wire loop has mass 𝑚 and radius 𝑟 and it is in a uniform vertical magnetic field \(B_0\), as shown in the figure. Initially, it hangs vertically downwards, because of acceleration due to gravity 𝑔, on two conducting supports at P and Q. When a current 𝐼 is passed through the loop, the loop turns about the line PQ by an angle 𝜃 given by

A thin stiff insulated metal wire is bent into a circular loop with its two ends extending tangentially from the same point of the loop. The wire loop has mass 𝑚 and radius 𝑟 and it is in a uniform vertical magnetic field \(B_0\), as shown in the figure. Initially, it hangs vertically downwards, because of acceleration due to gravity 𝑔, on two conducting supports at P and Q. When a current 𝐼 is passed through the loop, the loop turns about the line PQ by an angle 𝜃 given by


Updated On: Aug 13, 2024
- \(tan\theta = \frac{\pi rlB_0}{(𝑚𝑔)}\)
- \(tan\theta = \frac{2\pi rlB_0}{(𝑚𝑔)}\)
- \(tan\theta = \frac{\pi rlB_0}{(2𝑚𝑔)}\)
- \(tan\theta = \frac{mg}{(\pi rlB_0)}\)
Hide Solution
Verified By Collegedunia
The Correct Option is A
Solution and Explanation
The correct option is (A):\(tan\theta = \frac{\pi rlB_0}{(𝑚𝑔)}\)
Was this answer helpful?
0
2
Top Questions on Uniform Circular Motion
- A car of 800 kg is taking a turn on a banked road of radius 300 m and angle of banking 30°. If the coefficient of static friction is 0.2, then the maximum speed with which the car can negotiate the turn safely: (Given $g = 10 \, \text{m/s}^2$, $\sqrt{3} = 1.73$).
- JEE Main - 2024
- Physics
- Uniform Circular Motion
- A cyclist starts from the point P of a circular ground of radius 2 km and travels along its circumference to the point S. The displacement of a cyclist is :

- JEE Main - 2024
- Physics
- Uniform Circular Motion
- A particle moving with uniform speed in a circular path maintains :
- NEET (UG) - 2024
- Physics
- Uniform Circular Motion
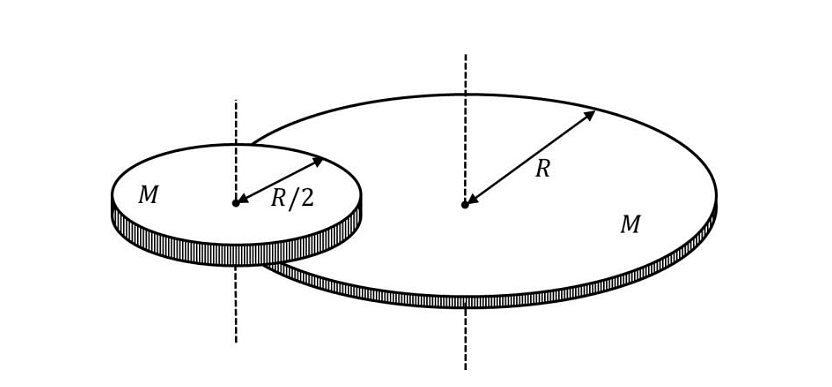
- A disc of mass \(M\) and radius \(R\) is free to rotate about its vertical axis as shown in the figure. A battery operated motor of negligible mass is fixed to this disc at a point on its circumference. Another disc of the same mass \(M\) and radius \(R/2\) is fixed to the motor’s thin shaft. Initially, both the discs are at rest. The motor is switched on so that the smaller disc rotates at a uniform angular speed \(\omega\). If the angular speed at which the large disc rotates is \(\omega/n\), then the value of \(n\) is _____
- JEE Advanced - 2024
- Physics
- Uniform Circular Motion
- A particle connected with light thread is performing vertical circular motion. Speed at point B (Lowermost point) is sufficient, so that it is able to complete its circular motion. Ignoring air friction, find the ratio of kinetic energy at A to that at B. (A being top-most point)

- JEE Main - 2024
- Physics
- Uniform Circular Motion
View More Questions
Questions Asked in JEE Advanced exam
- Let the function \(f:[1,\infin)→\R\) be defined by
\(f(t) = \begin{cases} (-1)^{n+1}2, & \text{if } t=2n-1,n\in\N, \\ \frac{(2n+1-t)}{2}f(2n-1)+\frac{(t-(2n-1))}{2}f(2n+1) & \text{if } 2n-1<t<2n+1,n\in\N. \end{cases}\)
Define \(g(x)=\int\limits_{1}^{x}f(t)dt,x\in(1,\infin).\) Let α denote the number of solutions of the equation g(x) = 0 in the interval (1, 8] and \(β=\lim\limits_{x→1+}\frac{g(x)}{x-1}\). Then the value of α + β is equal to _____.- JEE Advanced - 2024
- Integral Calculus
- A dimensionless quantity is constructed in terms of electronic charge \(e\), permittivity of free space \(\epsilon_0\) , Planck’s constant ℎ, and speed of light c. If the dimensionless quantity is written as \(e^\alpha\epsilon_0^\beta h^\gamma c^\delta\)and n is a non-zero integer, then\((\alpha, \beta,\gamma,\delta)\) is given by
- JEE Advanced - 2024
- Semiconductor electronics: materials, devices and simple circuits
- A block of mass \(5 kg\) moves along the \(x-\)direction subject to the force \(F = (−20x + 10) N,\) with the value of \(x \) in metre. At time \(t = 0 s,\) it is at rest at position \(x = 1 m\). The position and momentum of the block at \(t = (\pi/4)\) s are
- JEE Advanced - 2024
- Work-energy theorem
- A region in the form of an equilateral triangle (in x-y plane) of height L has a uniform magnetic field 𝐵⃗ pointing in the +z-direction. A conducting loop PQR, in the form of an equilateral triangle of the same height 𝐿, is placed in the x-y plane with its vertex P at x = 0 in the orientation shown in the figure. At 𝑡 = 0, the loop starts entering the region of the magnetic field with a uniform velocity 𝑣 along the +x-direction. The plane of the loop and its orientation remain unchanged throughout its motion.
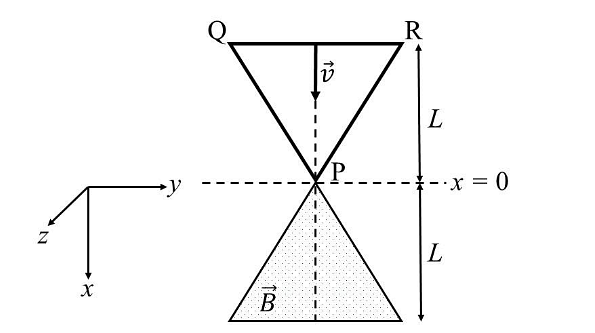
Which of the following graph best depicts the variation of the induced emf (E) in the loop as a function of the distance (𝑥) starting from 𝑥 = 0? - Two beads, each with charge q and mass m, are on a horizontal, frictionless, non-conducting, circular hoop of radius R. One of the beads is glued to the hoop at some point, while the other one performs small oscillations about its equilibrium position along the hoop. The square of the angular frequency of the small oscillations is given by [ \(\epsilon_0 \)is the permittivity of free space.]
- JEE Advanced - 2024
- Moving charges and magnetism
View More Questions



