A particle connected with light thread is performing vertical circular motion. Speed at point B (Lowermost point) is sufficient, so that it is able to complete its circular motion. Ignoring air friction, find the ratio of kinetic energy at A to that at B. (A being top-most point)
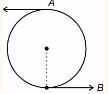

- \(1 : 5\)
- \(5 : 1\)
- \(1: 7\sqrt2\)
- \(1: 5\sqrt2\)
The Correct Option is A
Solution and Explanation
The correct option is (A): \(1 : 5\)
Top Questions on Uniform Circular Motion
- A car of 800 kg is taking a turn on a banked road of radius 300 m and angle of banking 30°. If the coefficient of static friction is 0.2, then the maximum speed with which the car can negotiate the turn safely: (Given $g = 10 \, \text{m/s}^2$, $\sqrt{3} = 1.73$).
- JEE Main - 2024
- Physics
- Uniform Circular Motion
- A cyclist starts from the point P of a circular ground of radius 2 km and travels along its circumference to the point S. The displacement of a cyclist is :

- JEE Main - 2024
- Physics
- Uniform Circular Motion
- A particle moving with uniform speed in a circular path maintains :
- NEET (UG) - 2024
- Physics
- Uniform Circular Motion
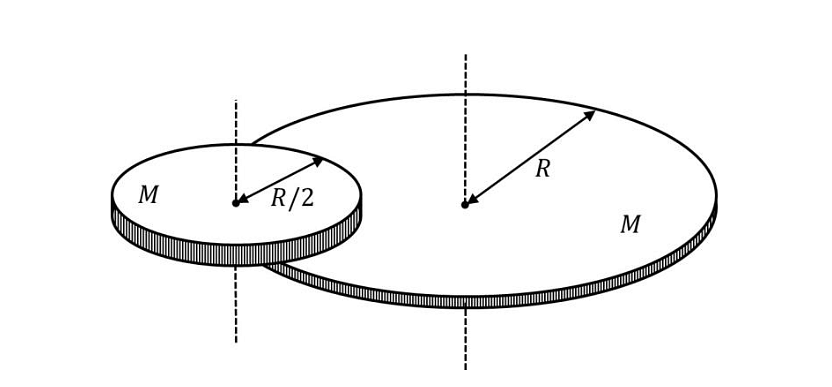
- A disc of mass \(M\) and radius \(R\) is free to rotate about its vertical axis as shown in the figure. A battery operated motor of negligible mass is fixed to this disc at a point on its circumference. Another disc of the same mass \(M\) and radius \(R/2\) is fixed to the motor’s thin shaft. Initially, both the discs are at rest. The motor is switched on so that the smaller disc rotates at a uniform angular speed \(\omega\). If the angular speed at which the large disc rotates is \(\omega/n\), then the value of \(n\) is _____
- JEE Advanced - 2024
- Physics
- Uniform Circular Motion
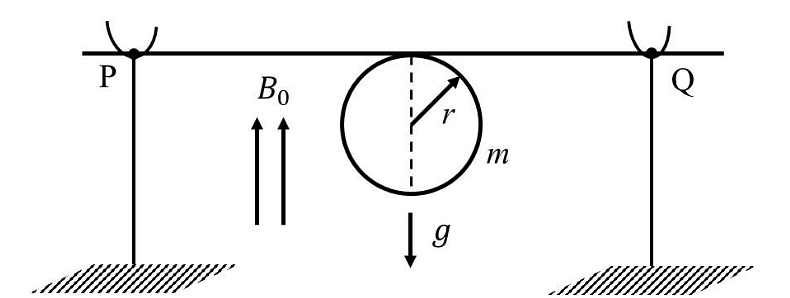
- A thin stiff insulated metal wire is bent into a circular loop with its two ends extending tangentially from the same point of the loop. The wire loop has mass 𝑚 and radius 𝑟 and it is in a uniform vertical magnetic field \(B_0\), as shown in the figure. Initially, it hangs vertically downwards, because of acceleration due to gravity 𝑔, on two conducting supports at P and Q. When a current 𝐼 is passed through the loop, the loop turns about the line PQ by an angle 𝜃 given by
- JEE Advanced - 2024
- Physics
- Uniform Circular Motion
Questions Asked in JEE Main exam
- Let \[\vec{a} = \hat{i} + \hat{j} + \hat{k}, \quad \vec{b} = -\hat{i} - 8\hat{j} + 2\hat{k}, \quad \text{and} \quad \vec{c} = 4\hat{i} + c_2\hat{j} + c_3\hat{k} \]be three vectors such that \[\vec{b} \times \vec{a} = \vec{c} \times \vec{a}.\]If the angle between the vector $\vec{c}$ and the vector $3\hat{i} + 4\hat{j} + \hat{k}$ is $\theta$, then the greatest integer less than or equal to $\tan^2 \theta$ is:
- JEE Main - 2024
- Vector Algebra
- 10 mL of gaseous hydrocarbon on combustion gives 40 mL of CO\(_2\)(g) and 50 mL of water vapour. The total number of carbon and hydrogen atoms in the hydrocarbon is ______ .
- JEE Main - 2024
- Hydrocarbons
- If each term of a geometric progression \( a_1, a_2, a_3, \dots \) with \( a_1 = \frac{1}{8} \) and \( a_2 \neq a_1 \), is the arithmetic mean of the next two terms and \( S_n = a_1 + a_2 + \dots + a_n \), then \( S_{20} - S_{18} \) is equal to
- JEE Main - 2024
- Arithmetic Mean
A body of mass 1000 kg is moving horizontally with a velocity of 6 m/s. If 200 kg extra mass is added, the final velocity (in m/s) is:
- JEE Main - 2024
- speed and velocity
- $\textbf{Choose the correct statements about the hydrides of group 15 elements.}$
A. The stability of the hydrides decreases in the order \(\text{NH}_3 > \text{PH}_3 > \text{AsH}_3 > \text{SbH}_3 > \text{BiH}_3\)
B. The reducing ability of the hydrides increases in the order \(\text{NH}_3 < \text{PH}_3 < \text{AsH}_3 < \text{SbH}_3 < \text{BiH}_3\)
C. Among the hydrides, \(\text{NH}_3\) is a strong reducing agent while \(\text{BiH}_3\) is a mild reducing agent.
D. The basicity of the hydrides increases in the order \(\text{NH}_3 < \text{PH}_3 < \text{AsH}_3 < \text{SbH}_3 < \text{BiH}_3\)
Choose the most appropriate from the option given below:- JEE Main - 2024
- p -Block Elements
Concepts Used:
Uniform Circular Motion
A circular motion is defined as the movement of a body that follows a circular route. The motion of a body going at a constant speed along a circular path is known as uniform circular motion. The velocity varies while the speed of the body in uniform circular motion remains constant.
Uniform Circular Motion Examples:
- The motion of electrons around its nucleus.
- The motion of blades of the windmills.
Uniform Circular Motion Formula:
When the radius of the circular path is R, and the magnitude of the velocity of the object is V. Then, the radial acceleration of the object is:
arad = v2/R
Similarly, this radial acceleration is always perpendicular to the velocity direction. Its SI unit is m2s−2.
The radial acceleration can be mathematically written using the period of the motion i.e. T. This period T is the volume of time taken to complete a revolution. Its unit is measurable in seconds.
When angular velocity changes in a unit of time, it is a radial acceleration.
Angular acceleration indicates the time rate of change of angular velocity and is usually denoted by α and is expressed in radians per second. Moreover, the angular acceleration is constant and does not depend on the time variable as it varies linearly with time. Angular Acceleration is also called Rotational Acceleration.
Angular acceleration is a vector quantity, meaning it has magnitude and direction. The direction of angular acceleration is perpendicular to the plane of rotation.
Formula Of Angular Acceleration
The formula of angular acceleration can be given in three different ways.
α = dωdt
Where,
ω → Angular speed
t → Time
α = d2θdt2
Where,
θ → Angle of rotation
t → Time
Average angular acceleration can be calculated by the formula below. This formula comes in handy when angular acceleration is not constant and changes with time.
αavg = ω2 - ω1t2 - t1
Where,
ω1 → Initial angular speed
ω2 → Final angular speed
t1 → Starting time
t2 → Ending time

Also Read: Angular Motion



