A circular disc of radius $R$ is removed from a bigger circular disc of radius $2 R$ such that the circumferences of the discs touch. The centre of mass of the new disc is at a distance $\alpha R$ from the centre of the bigger disc. The value of $\alpha$ is
- $\frac{1}{2}$
- $\frac{1}{3}$
- $\frac{1}{4}$
- $\frac{1}{6}$
The Correct Option is B
Solution and Explanation

Top Questions on Centre of mass
- Three blocks A, B and C are pulled on a horizontal smooth surface by a force of 80 N as shown in figure

The tensions T1 and T2 in the string are respectively:- JEE Main - 2024
- Physics
- Centre of mass
- Two solid spheres each of mass 2 kg and radius 75 cm are arranged as shown. Find MOI of the system about the given axis.
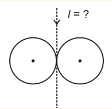
- JEE Main - 2024
- Physics
- Centre of mass
Find the value of m if \(M = 10\) \(kg\). All the surfaces are rough.
- JEE Main - 2024
- Physics
- Centre of mass
- Three identical spheres each of mass $M$ are placed at the corners of a right angled triangle with mutually perpendicular sides equal to $3 m$ each Taking point of intersection of mutually perpendicular sides as origin, the magnitude of position vector of centre of mass of the system will be $\sqrt{ x } m$ The value of $x$ is
- JEE Main - 2023
- Physics
- Centre of mass
As per the given figure, a small ball $P$ slides down the quadrant of a circle and hits the other ball $Q$ of equal mass which is initially at rest Neglecting the effect of friction and assume the collision to be elastic, the velocity of ball $Q$ after collision will be :$\left( g =10 \,m / s ^2\right)$
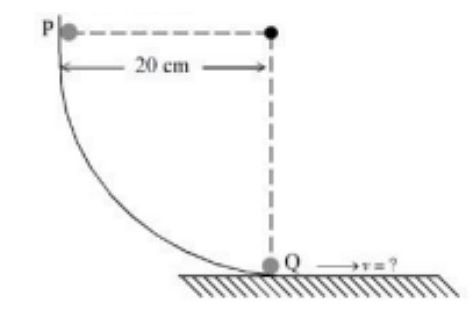
- JEE Main - 2023
- Physics
- Centre of mass
Questions Asked in EAMCET exam
- If $\quad \tan \theta \cdot \tan \left(120^{\circ}-\theta\right) \tan \left(120^{\circ}+\theta\right)=\frac{1}{\sqrt{3}}$, then $\theta$ is equal to
- EAMCET - 2015
- Trigonometric Equations
- If $f: R \rightarrow R, g: R \rightarrow R$ are defined by $f(x)=5\, x-3, g(x)=x^{2}+3$, then $g o f^{-1}(3)$ is equal to
- EAMCET - 2015
- Differentiability
- The common roots of the equations $z^{3}+2 z^{2}+2 z+1=0, z^{2014}+z^{2015}+1=0$ are
- EAMCET - 2015
- Quadratic Equations
- The value of the sum $1 \cdot 2 \cdot 3+2 \cdot 3 \cdot 4+3 \cdot 4 \cdot 5+\ldots$ upto $n$ terms is equal to
- EAMCET - 2015
- Sum of First n Terms of an AP
- The system $2\,x+3 y+z=5,3\,x+y+5\,z=7$ and $x+4\,y-2\,z=3$ has
- EAMCET - 2015
- Transpose of a Matrix
Concepts Used:
Center of Mass
The center of mass of a body or system of a particle is defined as a point where the whole of the mass of the body or all the masses of a set of particles appeared to be concentrated.
The formula for the Centre of Mass:

Center of Gravity
The imaginary point through which on an object or a system, the force of Gravity is acted upon is known as the Centre of Gravity of that system. Usually, it is assumed while doing mechanical problems that the gravitational field is uniform which means that the Centre of Gravity and the Centre of Mass is at the same position.



