1.0 g of magnesium is burnt with 0.56 g O2 in a closed vessel. Which reactant is left in excess and how much? (At. wt. Mg = 24 ; O = 16)
Show Hint
The equation is \(2Mg + O_2 → 2MgO\)
- Mg, 0.16 g
O2, 0.16 g
- Mg, 0.44 g
O2, 0.28 g
The Correct Option is A
Approach Solution - 1
The balanced chemical equation is \(\underset{\begin{smallmatrix} \\ \\ 24g \end{smallmatrix}}{\mathop{Mg}}\,+\underset{\begin{smallmatrix} \\ 16g \end{smallmatrix}}{\mathop{\frac{1}{2}{{O}_{2}}}}\,\xrightarrow{\,}\underset{\begin{smallmatrix} \\ \\ 40g \end{smallmatrix}}{\mathop{MgO}}\,\)
From the above equation, we note that 24 g Mg reacts with 16 g O2
Therefore, 1.0 g Mg reacts with \(\frac{16}{24}\times 0.67g\,{{O}_{2}}=0.67g\,{{O}_{2}}.\)
However, only 0.56 g of O2 is available.
Thus, O2 is the limiting reagent.
16 g O2 then reacts with 24 g Mg.
\(\therefore\) 0.56 g O2 will react with Mg \(=\frac{24}{16}\times 0.56=0.84g\)
The amount of Mg left unreacted = 1.0 - 0.84g Mg = 0.16g Mg.
Hence, Mg is present in excess and 0.16 g Mg is left behind unreacted.
So, the correct option is (A): Mg, 0.16 g
Approach Solution -2
The equation is \(2Mg + O_2 → 2MgO\)
(s) (g) (s)
Hence, 2 moles of Magnesium react with 1 mole of \(O_2\) to form 2 moles of MgO.
No. of moles = \(\frac {\text {Mass}}{\text {Molar\ Mass}}\)
- \(Mg \)= \(\frac {1}{24}\) = 0.041667
- \(O_2\) = \(\frac {0.56}{32}\) = 0.0175
The mole ratio of Mg: \(O_2\) = 2:1
This means that 2 moles of Mg react with 1 mole of \(O_2\)
Mass = Moles x Molar mass
= 24 x 0.035
= 0.84 g
Therefore, out of 1 gram of magnesium that reacts only 0.84 grams is used.
Hence, when 1.0 g of magnesium is burnt with 0.56 g \(O_2\) in a closed vessel, magnesium is present in excess by 0.16.
So, the correct option is (A): Mg, 0.16 g
Top Questions on Some basic concepts of chemistry
- A compound X contains 32% of A, 20% of B and remaining percentage of C. Then, the empirical formula of X is:
(Given atomic masses of A=64; B=40; C=32 u)- NEET (UG) - 2024
- Chemistry
- Some basic concepts of chemistry
- Following Kjeldahl's method, 1g of organic compound released ammonia that neutralized 10 mL of 2M H\(_2\)SO\(_4\). The percentage of nitrogen in the compound is _________.%.
- JEE Main - 2024
- Chemistry
- Some basic concepts of chemistry
- Match List I with List II
\(\begin{array}{|c|c|c|} \hline \text{LIST I (Technique)} & & \text{LIST II (Application)} \\ \hline \text{A. Distillation} & & \text{I. Separation of glycerol from spent-lye} \\ \text{B. Fractional distillation} & & \text{II. Aniline - Water mixture} \\ \text{C. Steam distillation} & & \text{III. Separation of crude oil fractions} \\ \text{D. Distillation under reduced pressure} & & \text{IV. Chloroform-Aniline} \\ \hline \end{array}\)
Choose the correct answer from the options given below:- JEE Main - 2024
- Chemistry
- Some basic concepts of chemistry
- The fragrance of flowers is due to the presence of some steam volatile organic compounds called essential oils. These are generally insoluble in water at room temperature but are miscible with water vapour in vapour phase. A suitable method for the extraction of these oils from the flowers is -
- JEE Main - 2024
- Chemistry
- Some basic concepts of chemistry
- The technique used for purification of steam volatile water immiscible substance is:
- JEE Main - 2024
- Chemistry
- Some basic concepts of chemistry
Questions Asked in NEET exam
- Which one of the following is not a criterion for classification of fungi?
- NEET (UG) - 2024
- Kingdom Fungi
- A parallel plate capacitor is charged by connecting it to a battery through a resistor. If I is the current in the circuit, then in the gap between the plates :
- NEET (UG) - 2024
- Capacitors and Capacitance
- Match List I with List II.Choose the correct answer from the options given below:
List I
(Spectral Lines of Hydrogen for transitions from)List II
(Wavelength (nm))A. n2 = 3 to n1 = 2 I. 410.2 B. n2 = 4 to n1 = 2 II. 434.1 C. n2 = 5 to n1 = 2 III. 656.3 D. n2 = 6 to n1 = 2 IV. 486.1 - NEET (UG) - 2024
- Bohr’s Model for Hydrogen Atom
- Match List I with List IIChoose the correct answer from the options given below
List-I List-II A Rhizopus I Mushroom B Ustilago II Smut fungus C Puccinia III Bread mould D Agaricus IV Rust fungus - NEET (UG) - 2024
- Nomenclature and taxonomy
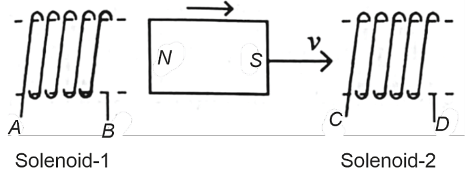
In the above diagram, a strong bar magnet is moving towards solenoid-2 from solenoid-1. The direction of induced current in solenoid-1 and that in solenoid-2, respectively, are through the directions :- NEET (UG) - 2024
- Solenoids and Toroids
Concepts Used:
Some Basic Concepts of Chemistry
Chemistry is a vast subject and for understanding its significance we can take help of following points:
- Chemistry plays an important role in understanding various subjects like physics, geology and biology.
- Chemistry is a core branch of science that explains us about the various compositional properties and interaction of matter. It also helps to understand various chemical reactions.
- Chemistry is important in order to understand the behaviour of fertilizers, alkenes, acids, salts, dyes, polymers, drugs, soaps and alloys in organic and inorganic chemistry.
- Chemistry plays an important role in various fields like healthcare, industrial, research, food, and farm activities.
Read More: Some Basic Concepts of Chemistry
Classification of Matter
There are two ways of classifying the matter:
(A) Physical Classification:
Matter can exist in three physical states:
- Solids - have definite volume and definite shape
- Liquids - have definite volume but not definite shape.
- Gases - have neither definite volume nor definite shape.
(B) Chemical Classification:
Based upon the composition, matter can be divided into two main types:
- Pure Substances are defined as a single substance (or matter) which cannot be separated by simple physical methods. Pure substances can be further classified as (i) Elements (ii) Compounds
- Mixtures are the combination of two or more elements or compounds which are not chemically combined together and may also be present in any proportion.