The values of $m, n$, for which the system of equations
$x + y + z = 4,$
$2x + 5y + 5z = 17,$
$x + 2y + mz = n$
has infinitely many solutions, satisfy the equation :
$x + y + z = 4,$
$2x + 5y + 5z = 17,$
$x + 2y + mz = n$
has infinitely many solutions, satisfy the equation :
- $m^{2} + n^{2} - m - n = 46$
- $m^{2} + n^{2} + m + n = 64$
- $m^{2} + n^{2} + mn = 68$
- $m^{2} + n^{2} - mn = 39$
The Correct Option is D
Solution and Explanation
To find the values of m and n such that the system has infinitely many solutions, we start by setting the determinant of the coefficient matrix to zero:
\[ D = \begin{vmatrix} 1 & 1 & 1 \\ 2 & 5 & 5 \\ 1 & 2 & m \end{vmatrix} = 0. \]
Expanding the determinant:
\[ D = 1 \cdot (5m - 10) - 1 \cdot (2m - 5) + 1 \cdot (4 - 5) = 3m - 6. \]
Setting \(D = 0\):
\[ 3m - 6 = 0 \implies m = 2. \]
Next, consider the augmented matrix determinant \(D_3\):
\[ D_3 = \begin{vmatrix} 1 & 1 & 4 \\ 2 & 5 & 17 \\ 1 & 2 & n \end{vmatrix} = 0. \]
Expanding \(D_3\) and setting it to zero gives:
\[ n = 7. \]
Substitute \(m = 2\) and \(n = 7\) into the given equation:
\[ m^2 + n^2 - mn = 2^2 + 7^2 - (2 \times 7) = 4 + 49 - 14 = 39. \]
Therefore, the correct answer is Option (4).
Top Questions on Linear Algebra
- Select all choices that are subspaces of \(\R^3\).
Note : \(\R\) denotes the set of real numbers. - Consider the system of linear equations \( x + y + z = 4\mu \), \( x + 2y + 2\lambda z = 10\mu \), \( x + 3y + 4\lambda^2 z = \mu^2 + 15 \), where \( \lambda, \mu \in \mathbb{R} \). Which one of the following statements is NOT correct?
- JEE Main - 2024
- Mathematics
- Linear Algebra
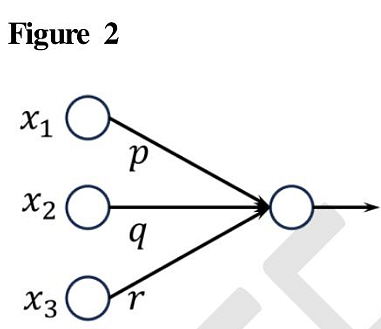
- Consider the two neural networks (NNs) shown in Figures 1 and 2, with ReLU activation (ReLU(z) = max{0, z}, ∀z ∈ R). R denotes the set of real numbers. The connections and their corresponding weights are shown in the Figures. The biases at every neuron are set to 0. For what values of p, q, r in Figure 2 are the two NNs equivalent, when x1, x2, x3 are positive ?

- Which of the following statements is/are TRUE ?
Note: \(\R\) denotes the set of real numbers. - Let \(\R\) be the set of real numbers, U be a subspace of \(\R^3\) and M ∈ \(\R^{3×3}\) be the matrix corresponding to the projection on to the subspace U.
Which of the following statements is/are TRUE ?
Questions Asked in JEE Main exam
- An artificial cell is made by encapsulating \(0.2 \, \text{M}\) glucose solution within a semipermeable membrane. The osmotic pressure developed when the artificial cell is placed within a \(0.05 \, \text{M}\) solution of NaCl at 300 K is ______ \( \times 10^{-1} \, \text{bar} \). (Nearest Integer)
Given: \(R = 0.083 \, \text{L bar mol}^{-1} \text{K}^{-1}\)
Assume complete dissociation of NaCl.- JEE Main - 2024
- Colligative Properties
- Let \[\vec{a} = \hat{i} + \hat{j} + \hat{k}, \quad \vec{b} = -\hat{i} - 8\hat{j} + 2\hat{k}, \quad \text{and} \quad \vec{c} = 4\hat{i} + c_2\hat{j} + c_3\hat{k} \]be three vectors such that \[\vec{b} \times \vec{a} = \vec{c} \times \vec{a}.\]If the angle between the vector $\vec{c}$ and the vector $3\hat{i} + 4\hat{j} + \hat{k}$ is $\theta$, then the greatest integer less than or equal to $\tan^2 \theta$ is:
- JEE Main - 2024
- Vector Algebra
- 10 mL of gaseous hydrocarbon on combustion gives 40 mL of CO\(_2\)(g) and 50 mL of water vapour. The total number of carbon and hydrogen atoms in the hydrocarbon is ______ .
- JEE Main - 2024
- Hydrocarbons
- If each term of a geometric progression \( a_1, a_2, a_3, \dots \) with \( a_1 = \frac{1}{8} \) and \( a_2 \neq a_1 \), is the arithmetic mean of the next two terms and \( S_n = a_1 + a_2 + \dots + a_n \), then \( S_{20} - S_{18} \) is equal to
- JEE Main - 2024
- Arithmetic Mean
A body of mass 1000 kg is moving horizontally with a velocity of 6 m/s. If 200 kg extra mass is added, the final velocity (in m/s) is:
- JEE Main - 2024
- speed and velocity



