The temperature of a gas is -50° C. To what temperature the gas should be heated so that the rms speed is increased by 3 times?
- 223 K
- 669°C
- 3295°C
- 3097 K
The Correct Option is C
Approach Solution - 1
We know that,
\(V_{rms}\propto \sqrt{T}\)
\(\frac{V_{1}}{V_{2}}=\sqrt{\frac{T_{1}}{T_{2}}}\)
\(⇒\) let the initial speed be \(v\).
As the speed increases by 3 times,
So, the final speed \(= 4v\)
\(⇒ \frac{v}{4v}\)
\(= \sqrt{\frac{223}{T}}\)
\(T=3568\text{ K}\)
So, the temperature in \(\degree{C} = 3568 - 273 = 3295\degree{C}\)
The correct answer is (C): \(3295°C\).
Approach Solution -2
The new velocity (V’rms) has been increased by 3 times the old velocity (Vrms).
Therefore, \(V’_{rms} = V_{rms} + 3 V_{rms} = 4V_{rms}\)
And, we also know Vrms is directly proportional to \(\sqrt{T}\)
Given, the initial temperature (T) = -50°C
Converting the temperature (T) to Kelvin: -50°C + 273 = 223K
Therefore initial temperature (T) in kelvin = 223K
If the speed increases to 4 times, the temperature should also increase by 16 times.
\(\frac{V’_{rms}}{V_{rms}} = \sqrt{\frac{T'}{T}}\)
\(\frac{4V_{rms}}{V_{rms}} = \sqrt \frac{T'}{223}\)
Therefore, Final Temperature (T’) \(= 16 \times 223 = 3568 K\)
Hence, Final Temperature (T’) in \(\degree C = 3568-273 = 3295 \degree C\)
So, the correct option is (C): \(3295 \degree C\)
Top Questions on kinetic theory
- When a system of multiple long narrow slits (width 2µm and period 4µm) is illuminated with a laser of wavelength 600nm. There are 40 minima between the two consecutive principal maxima observed in its diffraction pattern. Then maximum resolving power of the system is _______
- IIT JAM - 2024
- Physics
- kinetic theory
- A gas consists of particles, each having three translational and three rotational degrees of freedom. The ratio of specific heats, Cp/Cv, is: (Cp and Cv are the specific heats at constant pressure and constant volume, respectively).
- IIT JAM - 2024
- Physics
- kinetic theory
- A cylinder-piston system contains N atoms of an ideal gas. If 𝑡𝑎𝑣𝑔 is the average time between successive collisions of a given atom with other atoms. If the temperature T of the gas is increased isobarically, then 𝑡𝑎𝑣𝑔 is proportional to :
- IIT JAM - 2024
- Physics
- kinetic theory
- A one-dimensional infinite square-well potential is given by:
\(v(x)=0\,\,for\,\,-\frac{a}{2}<x<+\frac{a}{2}\)= ∞ elsewhere
Let 𝐸𝑒 (𝑥) and ψ𝑒 (𝑥) be the ground state energy and the corresponding wave function, respectively, if an electron (e) is trapped in that well. Similarly, let 𝐸µ(𝑥) and ψµ (𝑥) be the corresponding quantities, if a muon (µ) is trapped in the well. Choose the correct option:- IIT JAM - 2024
- Physics
- kinetic theory
- The Fermi energy of a system is 5.5eV. At 500K, the energy of a level for which the probability of occupancy is 0.2, is ________eV. (Rounded off to two decimal places) (Boltzmann constant 𝑘𝐵 = 8.62x10−5 eV/K)
- IIT JAM - 2024
- Physics
- kinetic theory
Questions Asked in NEET exam
- Which one of the following is not a criterion for classification of fungi?
- NEET (UG) - 2024
- Kingdom Fungi
- A parallel plate capacitor is charged by connecting it to a battery through a resistor. If I is the current in the circuit, then in the gap between the plates :
- NEET (UG) - 2024
- Capacitors and Capacitance
- Match List I with List II.Choose the correct answer from the options given below:
List I
(Spectral Lines of Hydrogen for transitions from)List II
(Wavelength (nm))A. n2 = 3 to n1 = 2 I. 410.2 B. n2 = 4 to n1 = 2 II. 434.1 C. n2 = 5 to n1 = 2 III. 656.3 D. n2 = 6 to n1 = 2 IV. 486.1 - NEET (UG) - 2024
- Bohr’s Model for Hydrogen Atom
- Match List I with List IIChoose the correct answer from the options given below
List-I List-II A Rhizopus I Mushroom B Ustilago II Smut fungus C Puccinia III Bread mould D Agaricus IV Rust fungus - NEET (UG) - 2024
- Nomenclature and taxonomy
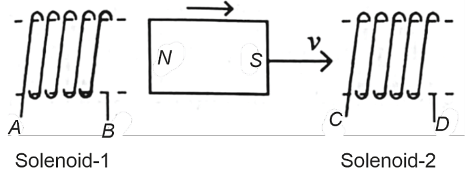
In the above diagram, a strong bar magnet is moving towards solenoid-2 from solenoid-1. The direction of induced current in solenoid-1 and that in solenoid-2, respectively, are through the directions :- NEET (UG) - 2024
- Solenoids and Toroids
Concepts Used:
Kinetic Theory of Gases & Formulae
Kinetic theory of ideal gases is based on the molecular picture of matter. An ideal gas is a gas that follows Boyle's law, Charles' law, Gay Lussac's law, and Avogadro’s law.
- Gases have no shape or size and can be contained in vessels of any shape and size.
- Since the molecule of the gases is apart from each other, they have a negligible force of molecular interaction.
- Therefore, gases expand indefinitely and uniformly to fill the available space.
- Many scientists like Boyle and Newton tried to explain the behavior of gases, but Maxwell and Boltzmann developed the real theory in the 19th century.
- This theory is known as the Kinetic theory, which explains the behavior of gases.
The kinetic Theory of Gases is a classical model of the thermodynamic behavior of gases, with which many principal concepts of thermodynamics were established. The kinetic theory of gases describes a gas as a large number of identical submicroscopic particles, all of which are in constant, random, rapid motion.
Also Read: Kinetic Theory of Gases - Assumptions
Kinetic Theory of Gas Formulae:
Boltzmann’s Constant
kB = nR/N
kB is the Boltzmann’s constant
R is the gas constant
n is the number of moles
N is the number of particles in one mole (the Avogadro number)
Total Translational K.E of Gas
K.E = (3/2)nRT
n is the number of moles
R is the universal gas constant
T is the absolute temperature
Maxwell Distribution Law
Vrms > V> Vp
Vrms is the RMS speed.
V is the Average speed.
Vp is the most probable speed.
RMS Speed (Vrms)
Vrms = \(\sqrt{8kt/m}\) =\(\sqrt{3RT/M}\)
R is the universal gas constant.
T is the absolute temperature.
M is the molar mass.
Average Speed
\(\overrightarrow{v} = \sqrt{8kt/πm} = \sqrt{8RT/πM}\)
Most Probable Speed (Vp)
\(V_ρ = \sqrt{2kt/m} = \sqrt{2RT/M}\)
The Pressure of Ideal Gas
\(P=\frac{1}{3}V^2rms\)
P is the density of molecules.
Equipartition of Energy
\(K=\frac{1}{2}K_BT\) for each degree of freedom.
K = (f/2) KвT for molecules having f degrees of freedom.
KB is the Boltzmann’s constant.
T is the temperature of the gas.
Internal Energy
U = (f/2) nRT
For n moles of an ideal gas.
Read About: Kinetic Theory of Gases Formulae