The function \(f(x) = \log(1+x) - \frac{2x}{2+x}\) is increasing on
- \((- \infty, \infty)\)
- \((- 1, \infty)\)
- \(( \infty, -1)\)
- \((- \infty, 0)\)
The Correct Option is B
Solution and Explanation
\(f(x) = \log(1+x) - \frac{2x}{2+x}\)
To simplify the expression, we can rewrite it as:
\(f(x) = \log(1+x) - \frac{2x}{2+x}\)
To find the derivative, we apply the logarithmic differentiation and the quotient rule:
\(f'(x) = \frac{1}{1+x} - 2\left(\frac{1}{2+x}\right) - 2x \left(-\frac{1}{(2+x)^2}\right)\)
Simplifying further:
\(f'(x) = \frac{1}{1+x} - \frac{2}{2+x} + \frac{2x}{(2+x)^2}\)
Now, we need to determine where \(f'(x) > 0.\)
To analyze the sign of f'(x), we can find the common denominator for the fractions:
\(f'(x) = \frac{(2+x)(2+x) - 2(1+x) + 2x}{(1+x)(2+x)^2}\)
Expanding the numerator:
\(f'(x) = \frac{4+4x+x^2 - 2 - 2x + 2x}{(1+x)(2+x)^2}\)
\(f'(x) = \frac{x^2}{(1+x)(2+x)^2}\)
Now, let's analyze the sign of f'(x) based on the numerator and denominator.
For the numerator, \(x^2\) is always non-negative.
For the denominator, \((1+x)\) and \((2+x)^2\) are also always non-negative, except when x = -1.
Therefore, f'(x) is positive (greater than zero) when \(x ≠ -1.\)
Hence, the function \(f(x) = \log(1+x) - \frac{2x}{2+x}\) is increasing on the interval \((-1, \infty)\), which corresponds to option (B) \((-1, \infty)\).
Top Questions on Exponential and Logarithmic Functions
- Let \(a=3\sqrt2\) and \(b=\frac{1}{5^{1/6}\sqrt5}\). If x, y ∈ R are such that
\(3x+2y=\log_a(18)^{\frac{5}{4}}\) and
\(2x-y=\log_b(\sqrt{1080})\),
then 4x + 5y is equal to _______.- JEE Advanced - 2024
- Mathematics
- Exponential and Logarithmic Functions
If (2,-1,3) is the foot of the perpendicular drawn from the origin to a plane, then the equation of that plane is
- TS EAMCET - 2023
- Mathematics
- Exponential and Logarithmic Functions
- The value of \(\frac{1}{\log_3{60}} + \frac{1}{\log_4{60}} + \frac{1}{\log_5{60}}\) is
- AP POLYCET - 2023
- Mathematics
- Exponential and Logarithmic Functions
- If \(y =\)\(e^{\sqrt{x\sqrt{x\sqrt{x\ldots}}}}\) \(x>1,\) then \(\left. \frac{{d^2y}}{{dx^2}} \right|_{x = \log_e 3}\) is
- KCET - 2022
- Mathematics
- Exponential and Logarithmic Functions
- The sum of all the real roots of the equation \((e^{2x} – 4)(6e^{2x} – 5e^x + 1) = 0\) is
- JEE Main - 2022
- Mathematics
- Exponential and Logarithmic Functions
Questions Asked in KCET exam
- A cubical Gaussian surface has side of length a = 10 cm. Electric field lines are parallel to x-axis as shown. The magnitudes of electric fields through surfaces ABCD and EFGH are 6kNC-1 and 9kNC-1 respectively. Then the total charge enclosed by the cube is
[Take ε0 = 9 × 10-12 Fm-1]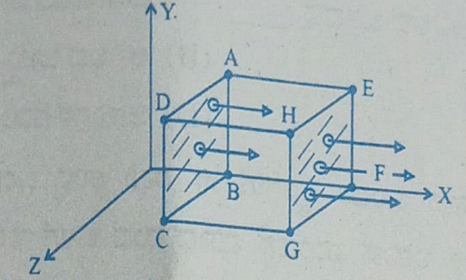
- KCET - 2023
- Gauss Law
- A sample of water is found to contain 5.85% \((\frac{w}{w})\) of AB (molecular mass 58.5) and 9.50% \((\frac{w}{w})\) XY2 (molecular mass 95). Assuming 80% ionisation of AB and 60% ionisation of XY2 , the freezing point of water sample is
[Given : Kf for water 1.86 K kg mol-1 , Freezing point of pure water is 273 K and A, B and Y are monovalent ions]- KCET - 2023
- Colligative Properties
- \(aMnO^{-}_4+bS_2O_{3}^-+H_2O\rightarrow xMnO_2+ySO_{4}^-+zOH^-\)
a and y respectively are- KCET - 2023
- Redox reactions
- \(\int\sqrt{\cosec x-\sin x}\ dx=\)
- KCET - 2023
- Definite Integral
- A metallic rod of length 1 m held along east-west direction is allowed to fall down freely. Given horizontal component of earth’s magnetic field BH = 3 × 10-5 T. The emf induced in the rod at an instant t = 2s after it is released is ( Take g = 10 ms-2 )
- KCET - 2023
- Faradays laws of induction



