The function \(f(x) = 4 \sin^3 x - 6 \sin^2 x + 12 \sin x + 100\) is strictly
- decreasing in \(\left[ - \frac{\pi}{2}, \frac{\pi}{2} \right]\)
- increasing in \([ \pi, \frac{3\pi}{2} ]\)
- decreasing in \([0, \frac{\pi}{2}]\)
- decreasing in \([\frac{\pi}{2}, \pi]\)
The Correct Option is D
Solution and Explanation
\(f(x) = 4 \sin^3(x) - 6 \sin^2(x) + 12 \sin(x) + 100\)
To find the derivative, we can use the chain rule and the power rule:
\(f'(x) = 3(4 \sin^2(x) \cos(x)) - 2(6 \sin(x) \cos(x)) + 12 \cos(x)\)
Simplifying further:
\(f'(x) = 12 \sin^2(x) \cos(x) - 12 \sin(x) \cos(x) + 12 \cos(x)\)
Now, to determine the intervals of increasing or decreasing, we need to analyze the sign of f'(x).
Let's analyze the sign of f'(x) in different intervals:
In the interval \([\frac{\pi}{2}, \pi]\)
For x values between \(\frac{\pi}{2}\) and \(π, sin(x)\) is positive, and cos(x) is negative.
Since \(sin^2(x)\) and \(cos(x) \) are non-negative, while sin(x) is positive, all terms in f'(x) are positive.
Therefore, f'(x) is always positive in this interval.
Thus, f(x) is strictly increasing in the interval \([\frac{\pi}{2}, \pi]\)
Based on the analysis, we can conclude that the function
\(f(x) = 4\sin^3(x) - 6\sin^2(x) + 12\sin(x) + 100\) is strictly increasing in the interval \([\frac{\pi}{2}, \pi]\), which corresponds to option (D) decreasing in \([\frac{\pi}{2}, \pi].\)
Top Questions on Trigonometric Identities
- Let \(\frac{\pi}{2}<x<\pi\) be such that \(\cot x=\frac{-5}{\sqrt{11}}\). Then
\((\sin\frac{11x}{2})(\sin 6x-\cos6x)+(\cos\frac{11x}{2})(\sin 6x+\cos 6x)\)
is equal to- JEE Advanced - 2024
- Mathematics
- Trigonometric Identities
- If \(f(x)\) = \(\begin {bmatrix} Cos x& -sinx & 0\\sinx & cos x& 0\\0&0&1 \end {bmatrix} \)Statement I \(⇒ f(x).f(y) = f(x+y)\) Statement II \(⇒f(-x) =0 \) is invertible
- JEE Main - 2024
- Mathematics
- Trigonometric Identities
- If sin2 θ+ cosec2 θ = 6, then sin θ + cosec θ =
- AP POLYCET - 2024
- Mathematics
- Trigonometric Identities
- If secθ+tanθ=k, then secθ-tanθ=?
- AP POLYCET - 2024
- Mathematics
- Trigonometric Identities
- If \(cos 2x-a \sin x=2a-7\) then range of \(a\) is:
- JEE Main - 2024
- Mathematics
- Trigonometric Identities
Questions Asked in KCET exam
- The current in a coil changes from 2A to 5A in 0.3s. The magnitude of emf induced in the coil is 1.0V. The value of self-inductance of the coil is
- KCET - 2023
- Electromagnetic induction
- A stretched wire of a material whose Young's modulus Y = 2 × 1011 Nm-2 has Poisson's ratio of 0.25. Its lateral strain εl = 10-3. The elastic energy density of the wire is
- KCET - 2023
- mechanical properties of solids
- A particle moves along the curve \(\frac{x^2}{16}+\frac{y^2}{4}=1\). When the rate of change of abscissa is 4 times that of its ordinate, then the quadrant in which the particle lies is
- KCET - 2023
- Conic sections
- A point object is moving at a constant speed of 1 ms-1 along the principal axis of a convex lens of focal length 10cm. The speed of the image is also 1 ms-1 , when the object is at _______ cm from the optic centre of the lens.
- KCET - 2023
- spherical lenses
- A cubical Gaussian surface has side of length a = 10 cm. Electric field lines are parallel to x-axis as shown. The magnitudes of electric fields through surfaces ABCD and EFGH are 6kNC-1 and 9kNC-1 respectively. Then the total charge enclosed by the cube is
[Take ε0 = 9 × 10-12 Fm-1]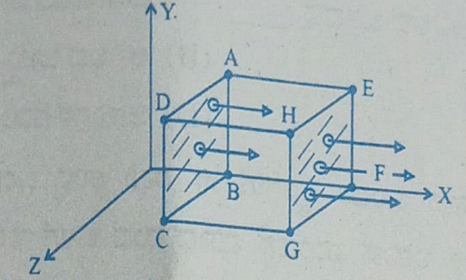
- KCET - 2023
- Gauss Law



