The electrical potential on the surface of a sphere of radius r due to a charge $ 3\times {{10}^{-6}}C $ is 500 V. The intensity of electric field on the surface of the sphere is $ \left[ \frac{1}{4\pi {{\varepsilon }_{0}}}=9\times {{10}^{9}}N{{m}^{2}}{{C}^{-2}} \right] $ $ (in\text{ }N{{C}^{-1}}) $ :
- $ <10 $
- >20
- Between 10 and 20
- <5
The Correct Option is A
Solution and Explanation
Top Questions on Gauss Law
- A charge q is placed at the center of one of the surface of a cube. The flux linked with the cube is :-
- JEE Main - 2024
- Physics
- Gauss Law
- An electric field \( \vec{E} = (2x \hat{i}) \, \text{N C}^{-1} \) exists in space. A cube of side \( 2 \, \text{m} \) is placed in the space as per the figure given below. The electric flux through the cube is __________ \( \text{N m}^2/\text{C} \).
- JEE Main - 2024
- Physics
- Gauss Law
- There are two cubical Gaussian surface carrying charges as shown. Find ratio of fluxes through surface \(C_1\) and \(C_2\):

- JEE Main - 2024
- Physics
- Gauss Law
- A cubical Gaussian surface has side of length a = 10 cm. Electric field lines are parallel to x-axis as shown. The magnitudes of electric fields through surfaces ABCD and EFGH are 6kNC-1 and 9kNC-1 respectively. Then the total charge enclosed by the cube is
[Take ε0 = 9 × 10-12 Fm-1]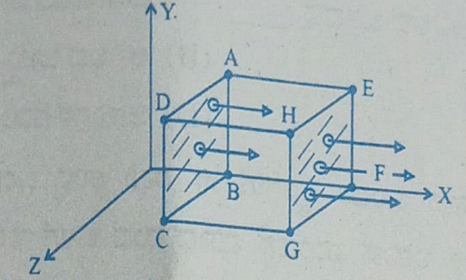
- KCET - 2023
- Physics
- Gauss Law
A cubical volume is bounded by the surfaces $x=0, x= a , y=0, y= a , z=0, z= a$ The electric field in the region is given by $\vec{E}=E_0 x \hat{ t }$ Where $E_0=4 \times 10^4 NC ^{-1} m ^{-1}$ If $a=2 cm$, the charge contained in the cubical volume is $Q \times 10^{-14} C$ The value of $Q$ is ___ Take \(E_{0}=9\times 10^{-2}C^{2}/Nm^{2}\)
- JEE Main - 2023
- Physics
- Gauss Law
Questions Asked in EAMCET exam
- If $\quad \tan \theta \cdot \tan \left(120^{\circ}-\theta\right) \tan \left(120^{\circ}+\theta\right)=\frac{1}{\sqrt{3}}$, then $\theta$ is equal to
- EAMCET - 2015
- Trigonometric Equations
- If $f: R \rightarrow R, g: R \rightarrow R$ are defined by $f(x)=5\, x-3, g(x)=x^{2}+3$, then $g o f^{-1}(3)$ is equal to
- EAMCET - 2015
- Differentiability
- The common roots of the equations $z^{3}+2 z^{2}+2 z+1=0, z^{2014}+z^{2015}+1=0$ are
- EAMCET - 2015
- Quadratic Equations
- The value of the sum $1 \cdot 2 \cdot 3+2 \cdot 3 \cdot 4+3 \cdot 4 \cdot 5+\ldots$ upto $n$ terms is equal to
- EAMCET - 2015
- Sum of First n Terms of an AP
- The system $2\,x+3 y+z=5,3\,x+y+5\,z=7$ and $x+4\,y-2\,z=3$ has
- EAMCET - 2015
- Transpose of a Matrix
Concepts Used:
Gauss Law
Gauss law states that the total amount of electric flux passing through any closed surface is directly proportional to the enclosed electric charge.
Gauss Law:
According to the Gauss law, the total flux linked with a closed surface is 1/ε0 times the charge enclosed by the closed surface.

For example, a point charge q is placed inside a cube of edge ‘a’. Now as per Gauss law, the flux through each face of the cube is q/6ε0.
Gauss Law Formula:
As per the Gauss theorem, the total charge enclosed in a closed surface is proportional to the total flux enclosed by the surface. Therefore, if ϕ is total flux and ϵ0 is electric constant, the total electric charge Q enclosed by the surface is;
Q = ϕ ϵ0
The Gauss law formula is expressed by;
ϕ = Q/ϵ0
Where,
Q = total charge within the given surface,
ε0 = the electric constant.



