Suppose the gravitational force varies inversely as the nth power of distance. Then, the time period of a planet in circular orbit of radius R around the sun will be proportional to
- $ R^{\left(\frac{n+1}{2}\right)} $
- $ R^{\left(\frac{n-1}{2}\right)} $
- $ R^n $
- $ R^{\left(\frac{n-2}{2}\right)} $
The Correct Option is A
Approach Solution - 1
$=$ gravitational force exerted on it
i.e., $\frac{mv^{2}}{R} = \frac{GM_{e} m}{R^{n}}$
$ v = \left(\frac{GM_{e}}{R^{n-1}}\right)^{1/2}$
Now, $T = \frac{2\pi R}{v} = 2\pi R \times \left(\frac{R^{n-1}}{GM_{e}}\right)^{1/2}$
$ \Rightarrow 2\pi \left(\frac{R^{2} \times R^{n-1}}{GM_{e}}\right)^{1/2} $
$T = 2\pi\left(\frac{R^{\left(n+1\right)/2}}{\left(GM_{e}\right)^{1/2}}\right) $
$\therefore T \propto R^{\left(n+1\right)/2}$
Approach Solution -2
The gravitational force typically varies inversely as the square of the distance (\( n = 2 \)) according to Newton's law of universal gravitation. However, if the gravitational force varies inversely as the \( n \)-th power of the distance, the relationship between the time period \( T \) of a planet in a circular orbit of radius \( R \) and the radius \( R \) itself will change.
Let's denote the force as:
\[ F \propto \frac{1}{R^n} \]
Step-by-Step Solution:
1. Expression for the Gravitational Force:
The gravitational force between two masses \( M \) (mass of the Sun) and \( m \) (mass of the planet) at a distance \( R \) can be written as:
\[ F = \frac{kMm}{R^n} \]
where \( k \) is a constant of proportionality.
2. Centripetal Force and Orbital Motion:
For a planet in a circular orbit, the gravitational force provides the necessary centripetal force to keep the planet in orbit. Therefore,
\[ \frac{kMm}{R^n} = \frac{mv^2}{R} \]
where \( v \) is the orbital speed of the planet.
3. Orbital Speed:
Solving for \( v \):
\[ \frac{kM}{R^n} = \frac{v^2}{R} \]
\[ v^2 = \frac{kM}{R^{n-1}} \]
\[ v = \sqrt{\frac{kM}{R^{n-1}}} \]
4. Orbital Period:
The time period \( T \) of the planet is the time it takes to complete one full orbit, which is the circumference of the orbit divided by the orbital speed:
\[ T = \frac{2\pi R}{v} \]
Substituting \( v \) from above:
\[ T = \frac{2\pi R}{\sqrt{\frac{kM}{R^{n-1}}}} \]
\[ T = \frac{2\pi R}{\sqrt{kM} \cdot R^{\frac{1-n}{2}}} \]
\[ T = \frac{2\pi R^{\frac{n+1}{2}}}{\sqrt{kM}} \]
5. Proportionality:
Ignoring the constants \( 2\pi \) and \( \sqrt{kM} \), the time period \( T \) is proportional to:
\[ T \propto R^{\frac{n+1}{2}} \]
Conclusion:
The time period \( T \) of a planet in a circular orbit of radius \( R \) around the sun, when the gravitational force varies inversely as the \( n \)-th power of the distance, is proportional to \( R^{\frac{n+1}{2}} \).
Hence the correct Answer is Option(A)(1): \( R^{\frac{n+1}{2}} \)
Top Questions on Centripetal forces
- A particle of mass 𝑚 is under the influence of the gravitational field of a body of mass 𝑀 (≫ 𝑚). The particle is moving in a circular orbit of radius \(𝑟_0\) with time period \(𝑇_0\) around the mass 𝑀. Then, the particle is subjected to an additional central force, corresponding to the potential energy 𝑉c(𝑟) = 𝑚𝛼/𝑟 3 , where 𝛼 is a positive constant of suitable dimensions and 𝑟 is the distance from the center of the orbit. If the particle moves in the same circular orbit of radius\( 𝑟_0\) in the combined gravitational potential due to 𝑀 and 𝑉c(𝑟), but with a new time period \(𝑇_1\), then\( (𝑇_1^2 − 𝑇_0^ 2 )/𝑇_1^ 2\) is given by [𝐺 is the gravitational constant.]
- JEE Advanced - 2024
- Physics
- Centripetal forces
- A particle of mass m is moving in a circular orbit under the influence of the central force\( f(r) = −kr\), corresponding to the potential energy \(v(r) = \frac{kr^2}{2}\), where \(k\) is a positive force constant and \( r\) is the radial distance from the origin. According to the Bohr’s quantization rule, the angular momentum of the particle is given by \(L= nℏ\), where\( ℏ = ℎ/(2pi), ℎ\) is the Planck’s constant, and \(n\) a positive integer. If \(v\) and \(E\) are the speed and total energy of the particle, respectively, then which of the following expression(s) is(are) correct?
- JEE Advanced - 2024
- Physics
- Centripetal forces
- A ball is released from rest from point P of a smooth semi-spherical vessel as shown in figure. The ratio of the centripetal force and normal reaction on the ball at point Q is A while angular position of point Q is α with respect to point P. Which of the following graphs represent the correct relation between A and α when ball goes from Q to R?

- JEE Main - 2022
- Physics
- Centripetal forces
- A toy car of mass 80g is maintained to move in a horizontal circle of radius 0.8m with a velocity v ms-1. If the centripetal force acting on it is 10 N, then the value of v in ms-1 is
- KEAM - 2022
- Physics
- Centripetal forces
- One end of a string of length ‘ l ’ is connected to a particle of mass ‘m’ and the other to a small peg on a smooth horizontal table. If the particle moves in a circle with speed ‘v’, the net force on the particle (directed towards the centre) is : (T is the tension in the string)
- KCET - 2020
- Physics
- Centripetal forces
Questions Asked in JEE Advanced exam
- A region in the form of an equilateral triangle (in x-y plane) of height L has a uniform magnetic field 𝐵⃗ pointing in the +z-direction. A conducting loop PQR, in the form of an equilateral triangle of the same height 𝐿, is placed in the x-y plane with its vertex P at x = 0 in the orientation shown in the figure. At 𝑡 = 0, the loop starts entering the region of the magnetic field with a uniform velocity 𝑣 along the +x-direction. The plane of the loop and its orientation remain unchanged throughout its motion.
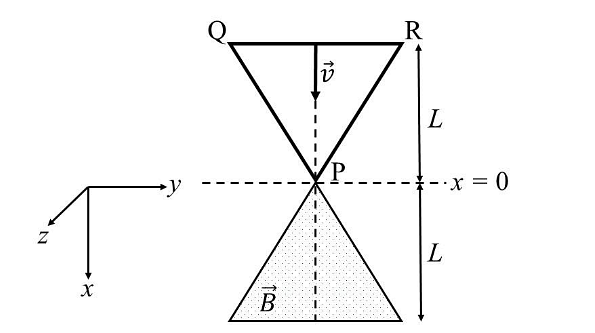
Which of the following graph best depicts the variation of the induced emf (E) in the loop as a function of the distance (𝑥) starting from 𝑥 = 0? - Two beads, each with charge q and mass m, are on a horizontal, frictionless, non-conducting, circular hoop of radius R. One of the beads is glued to the hoop at some point, while the other one performs small oscillations about its equilibrium position along the hoop. The square of the angular frequency of the small oscillations is given by [ \(\epsilon_0 \)is the permittivity of free space.]
- JEE Advanced - 2024
- Moving charges and magnetism
- A group of 9 students, s1, s2,…., s9, is to be divided to form three teams X, Y and Z of sizes 2, 3, and 4, respectively. Suppose that s1 cannot be selected for the team X and s2 cannot be selected for the team Y. Then the number of ways to form such teams, is _______.
- JEE Advanced - 2024
- Combinations
- Let \(\vec{p}=2\hat{i}+\hat{j}+3\hat{k}\) and \(\vec{q}=\hat{i}-\hat{j}+\hat{k}\). If for some real numbers α, β and γ we have
\(15\hat{i}+10\hat{j}+6\hat{k}=α(2\vec{p}+\vec{q})+β(\vec{p}-2\vec{q})+γ(\vec{p}\times\vec{q})\),
then the value of γ is ________.- JEE Advanced - 2024
- Vector Algebra
- Let X be a random variable, and let P(X = x) denote the probability that X takes the value x. Suppose that the points (x, P(X = x)), x = 0,1,2,3,4, lie on a fixed straight line in the xy -plane, and P(X = x) = 0 for all x ∈ R - {0,1,2,3,4}. If the mean of X is \(\frac{5}{2}\) , and the variance of X is α, then the value of 24α is ______.
- JEE Advanced - 2024
- Probability
Concepts Used:
Centripetal Forces
- The centripetal force makes a move on the object traveling in a circular direction and is directed towards the center upon which the object is moving.
- Centripetal force emanates from the gravitational pull and electrostatic force.
- It is a real force acting on both inertial frames and non-inertial frames.
- The centripetal force formula is

- From the object to the center is the exact direction of centripetal forces.
- The centripetal force has the tendency to turn towards the center.
- Centripetal force makes us set foot in a circular motion.



