Select Goal &
City
Select Goal
Explore
Question:
Let $X$ and $Y$ be two arbitrary, $3 \times 3$, non-zero, skew-symmetric matrices and $Z$ be an arbitrary $3 \times 3$, nonzero, symmetric matrix. Then which of the following matrices is (are) skew symmetric ?
Let $X$ and $Y$ be two arbitrary, $3 \times 3$, non-zero, skew-symmetric matrices and $Z$ be an arbitrary $3 \times 3$, nonzero, symmetric matrix. Then which of the following matrices is (are) skew symmetric ?
Updated On: Jun 14, 2022
- $Y^3Z^4 - Z^4Y^3$
- $X^{44} + Y^{44}$
- $X^4Z^3 - Z^3X^4$
- $X^{23} + Y^{23}$
Hide Solution
Verified By Collegedunia
The Correct Option is D
Solution and Explanation
$X^{T} = -X Y^{T} = -Y Z^{T} = Z$
$\left(A\right) \left(Y^{3} Z^{4} - Z^{4} Y^{3}\right)^{T} = \left(Y^{3} Z^{4}\right)^{T }- \left(Z^{4} Y^{3}\right)^{T}$
$= \left(Z^{4}\right)^{T} \left(Y^{3}\right)^{T }- \left(Y^{3}\right)^{T} \left(Z^{4}\right)^{T}$
$= \left(Z^{T}\right)^{4} \left(Y^{T}\right)^{3} - \left(Y^{T}\right)^{3} \left(Z^{T}\right)^{4}$
$= Z^{4 }\left(-Y\right)^{3} - \left(-Y\right)^{3} \left(Z\right)^{4}$
$= -Z^{4}Y^{3} + Y^{3} Z^{4}$
$= Y^{3}Z^{4} - Z^{4}Y^{3}$
Hence it is symmetric matrix.
$\left(B\right) \left(X^{44} + Y^{44}\right)^{T} = \left(X^{T}\right)^{44} + \left(Y^{T}\right)^{44}$
$= X^{44} + Y^{44}$
Hence it is symmetric matrix.
$\left(C\right) \left(X^{4} Z^{3} - Z^{3} X^{4}\right)^{T} = \left(X^{4} Z^{3}\right)^{T} - \left(Z^{3} X^{4}\right)^{T}$
$= \left(Z^{T}\right)^{3} \left(X^{T}\right)^{4} - \left(X^{T}\right)^{4} \left(Z^{T}\right)^{3}$
$= Z^{3} X^{4} - X^{4 }Z^{3}$
$= - \left(X^{4 }Z^{3} - Z^{3} X^{4}\right)$
Hence it is skew symmetric matrix.
$\left(D\right) \left(X^{23} + Y^{23}\right)^{T} = \left(X^{T}\right)^{23} + \left(Y^{T}\right)^{23}$
$= - \left(X^{23} + Y^{23}\right)$
Hence it is skew symmetric matrix.
$\left(A\right) \left(Y^{3} Z^{4} - Z^{4} Y^{3}\right)^{T} = \left(Y^{3} Z^{4}\right)^{T }- \left(Z^{4} Y^{3}\right)^{T}$
$= \left(Z^{4}\right)^{T} \left(Y^{3}\right)^{T }- \left(Y^{3}\right)^{T} \left(Z^{4}\right)^{T}$
$= \left(Z^{T}\right)^{4} \left(Y^{T}\right)^{3} - \left(Y^{T}\right)^{3} \left(Z^{T}\right)^{4}$
$= Z^{4 }\left(-Y\right)^{3} - \left(-Y\right)^{3} \left(Z\right)^{4}$
$= -Z^{4}Y^{3} + Y^{3} Z^{4}$
$= Y^{3}Z^{4} - Z^{4}Y^{3}$
Hence it is symmetric matrix.
$\left(B\right) \left(X^{44} + Y^{44}\right)^{T} = \left(X^{T}\right)^{44} + \left(Y^{T}\right)^{44}$
$= X^{44} + Y^{44}$
Hence it is symmetric matrix.
$\left(C\right) \left(X^{4} Z^{3} - Z^{3} X^{4}\right)^{T} = \left(X^{4} Z^{3}\right)^{T} - \left(Z^{3} X^{4}\right)^{T}$
$= \left(Z^{T}\right)^{3} \left(X^{T}\right)^{4} - \left(X^{T}\right)^{4} \left(Z^{T}\right)^{3}$
$= Z^{3} X^{4} - X^{4 }Z^{3}$
$= - \left(X^{4 }Z^{3} - Z^{3} X^{4}\right)$
Hence it is skew symmetric matrix.
$\left(D\right) \left(X^{23} + Y^{23}\right)^{T} = \left(X^{T}\right)^{23} + \left(Y^{T}\right)^{23}$
$= - \left(X^{23} + Y^{23}\right)$
Hence it is skew symmetric matrix.
Was this answer helpful?
0
0
Top Questions on Matrices
- If \(|2A|^3 =21\) and \(\begin{bmatrix} 1 & 0 & 0 \\[0.3em] 0 & α & β \\[0.3em] 0 & β & α \end{bmatrix}\), then a is (if \(α,β∈I\))
- Consider the 4 × 4 matrix
\(M = \begin{pmatrix} 0 & 1 & 2 & 3 \\ 1 & 0 & 1 & 2 \\ 2 & 1 & 0 & 1 \\ 3 & 2 & 1 & 0 \end{pmatrix}\)
If ai,j denotes the (i, j)th entry of M-1 , then a4,1 equals __________ (rounded off to two decimal places). - Let A be a 6 × 5 matrix with entries in ℝ and B be a 5 × 4 matrix with entries in ℝ. Consider the following two statements.
P : For all such nonzero matrices A and B, there is a nonzero matrix Z such that AZB is the 6 × 4 zero matrix.
Q : For all such nonzero matrices A and B, there is a nonzero matrix Y such that BYA is the 5 × 5 zero matrix.
Which one of the following holds ? - Let \(a=\begin{bmatrix} \frac{1}{\sqrt3} \\ \frac{-1}{\sqrt2} \\ \frac{1}{\sqrt6} \\ 0\end{bmatrix}\). Consider the following two statements.
P : The matrix I4 - aaT is invertible.
Q: The matrix I4 - 2aaT is invertible.
Then, which one of the following holds ? - Let \(S=\left\{\begin{pmatrix} 0 & 1 & c \\ 1 & a & d\\ 1 & b & e \end{pmatrix}:a,b,c,d,e\in\left\{0,1\right\}\ \text{and} |A|\in \left\{-1,1\right\}\right\}\), where |A| denotes the determinant of A. Then the number of elements in S is _______.
View More Questions
Questions Asked in JEE Advanced exam
- A region in the form of an equilateral triangle (in x-y plane) of height L has a uniform magnetic field 𝐵⃗ pointing in the +z-direction. A conducting loop PQR, in the form of an equilateral triangle of the same height 𝐿, is placed in the x-y plane with its vertex P at x = 0 in the orientation shown in the figure. At 𝑡 = 0, the loop starts entering the region of the magnetic field with a uniform velocity 𝑣 along the +x-direction. The plane of the loop and its orientation remain unchanged throughout its motion.
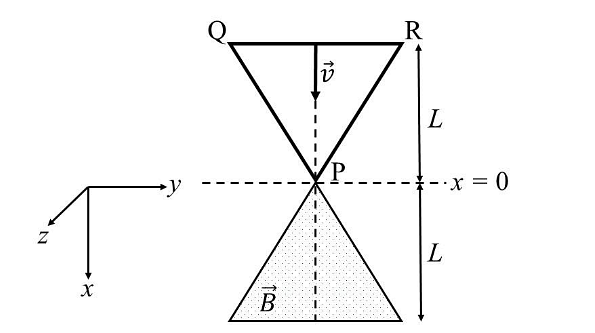
Which of the following graph best depicts the variation of the induced emf (E) in the loop as a function of the distance (𝑥) starting from 𝑥 = 0? - Two beads, each with charge q and mass m, are on a horizontal, frictionless, non-conducting, circular hoop of radius R. One of the beads is glued to the hoop at some point, while the other one performs small oscillations about its equilibrium position along the hoop. The square of the angular frequency of the small oscillations is given by [ \(\epsilon_0 \)is the permittivity of free space.]
- JEE Advanced - 2024
- Moving charges and magnetism
- A group of 9 students, s1, s2,…., s9, is to be divided to form three teams X, Y and Z of sizes 2, 3, and 4, respectively. Suppose that s1 cannot be selected for the team X and s2 cannot be selected for the team Y. Then the number of ways to form such teams, is _______.
- JEE Advanced - 2024
- Combinations
- Let \(\vec{p}=2\hat{i}+\hat{j}+3\hat{k}\) and \(\vec{q}=\hat{i}-\hat{j}+\hat{k}\). If for some real numbers α, β and γ we have
\(15\hat{i}+10\hat{j}+6\hat{k}=α(2\vec{p}+\vec{q})+β(\vec{p}-2\vec{q})+γ(\vec{p}\times\vec{q})\),
then the value of γ is ________.- JEE Advanced - 2024
- Vector Algebra
- Let X be a random variable, and let P(X = x) denote the probability that X takes the value x. Suppose that the points (x, P(X = x)), x = 0,1,2,3,4, lie on a fixed straight line in the xy -plane, and P(X = x) = 0 for all x ∈ R - {0,1,2,3,4}. If the mean of X is \(\frac{5}{2}\) , and the variance of X is α, then the value of 24α is ______.
- JEE Advanced - 2024
- Probability
View More Questions
Concepts Used:
Matrices
Matrix:
A matrix is a rectangular array of numbers, variables, symbols, or expressions that are defined for the operations like subtraction, addition, and multiplications. The size of a matrix is determined by the number of rows and columns in the matrix.
The basic operations that can be performed on matrices are:
- Addition of Matrices - The addition of matrices addition can only be possible if the number of rows and columns of both the matrices are the same.
- Subtraction of Matrices - Matrices subtraction is also possible only if the number of rows and columns of both the matrices are the same.
- Scalar Multiplication - The product of a matrix A with any number 'c' is obtained by multiplying every entry of the matrix A by c, is called scalar multiplication.
- Multiplication of Matrices - Matrices multiplication is defined only if the number of columns in the first matrix and rows in the second matrix are equal.
- Transpose of Matrices - Interchanging of rows and columns is known as the transpose of matrices.
SUBSCRIBE TO OUR NEWS LETTER
COLLEGE NOTIFICATIONSEXAM NOTIFICATIONSNEWS UPDATES
Download the Collegedunia app on 
© 2024 Collegedunia Web Pvt. Ltd. All Rights Reserved