Let $f\left(x\right) = sin\left(\frac{\pi}{6}sin\left(\frac{\pi}{2}sin\,x\right)\right)$ for all $x \in R$ and $g\left(x\right) = \frac{\pi}{2}$ $sin\, x$ for all $x \in R$. Let $(fog) (x)$ denote $f(g(x))$ and $(gof) (x)$ denote $g(f(x))$. Then which of the following is (are) true ?
- Range of $f$ is $\left[-\frac{1}{2}, \frac{1}{2}\right]$
- Range of $fog$ is $\left[-\frac{1}{2}, \frac{1}{2}\right]$
- $\displaystyle \lim_{x \to 0} \frac{f \left(x\right)}{g\left(x\right)} = \frac{\pi}{6}$
- There is an $x \in R$ such that $(gof)(x) = 1$
The Correct Option is C
Solution and Explanation
$- 1 \le sin x \le 1 as x ? R$
$-\frac{\pi}{2} \le \frac{\pi}{2} sinx \le \frac{\pi}{2}$
$-1 \le sin\left(\frac{\pi}{2}sin\, x\right)\le 1$
$-\frac{\pi}{6} \le \frac{\pi}{6} sin \left(\frac{\pi}{2}sin\, x\right) \le \frac{\pi}{6}$
$-\frac{1}{2}\le sin\left(\frac{\pi}{6}sin\left(\frac{\pi}{2}sin\, x\right)\right) \le \frac{1}{2}$
Range $?\left[-\frac{1}{2}, \frac{1}{2}\right]$
So option $\left(A\right)$ is correct.
f o g(x)
Range of g(x) $= \left[-\frac{\pi}{2}, \frac{\pi}{2}\right] n$ Domain of f(x) = R
Common $= \left[-\frac{\pi }{2}, \frac{\pi }{2}\right]$
Range of fog(x) = Range of f(x) when input $\left[-\frac{\pi }{2}, \frac{\pi }{2}\right]$
$= \left[-\frac{1}{2}, \frac{1}{2}\right]$
So option (B) is correct
$\displaystyle \lim_{x\to0} \frac{sin\left(\frac{\pi}{6}sin\left(\frac{\pi}{2}sin\, x\right)\right)}{\frac{\pi}{2}sin\, x} = \displaystyle \lim_{x\to 0} \left(\frac{sin\left(\frac{\pi }{6}sin\left(\frac{\pi }{2}sin\, x\right)\right)}{\frac{\pi }{6}sin\left(\frac{\pi }{2}sin\, x\right)}\right)\left(\frac{\frac{\pi }{6}sin\left(\frac{\pi }{2}sin\, x\right)}{\left(\frac{\pi}{2}sin\, x\right)}\right)$
$= \displaystyle \lim_{x\to 0} \frac{\pi}{6}.\left(1\right) = \frac{\pi}{6}$
So option $\left(B\right)$ is correct
g o f(x)
Range of f(x) $= \left[-\frac{1}{2}, \frac{1}{2}\right]$
g o f(x) $= \frac{\pi}{2}sin f\left(x\right)$
$= \frac{\pi}{2}sin\frac{\left(sin \left(\frac{\pi}{6}sin \left(\frac{\pi}{2} sin \,x\right)\right)\right) = 1}{\frac{1}{2} to \frac{1}{2}}$
$sin\left(\frac{1}{2} to \frac{1}{2}\right) = \frac{2}{\pi}\approx0.6379$ (not possible)
$\frac{1}{2} \approx 28.5^{\circ}$
So option $\left(D\right)$ is not correct.
Top Questions on Functions
- If the domain of the function \(f(x)\) = \(\frac{\sqrt{x^2-25}}{(4-x^2)}+ \log(x^2+2x-15)\) is \((-∞, α) ∪ (β, ∞)\), then \(α^2+β^2\) is equal to \(b\)
- Let the function \(f:\R→\R\) be defined by
\(f(x)=\frac{\sin x}{e^{\pi x}}\frac{(x)^{2023}+2024x+2025}{(x^2-x+3)}+\frac{2}{e^{\pi x}}\frac{(x^{2023}+2024x+2025)}{(x^2-x+3)}\)
Then the number of solutions of f (x) = 0 in \(\R\) is __. - Let \(f:[0,\frac{\pi}{2}]→[0,1]\) be the function defined by \(f(x)=\sin^2x\) and let \(g:[0,\frac{\pi}{2}]→[0,\infin)\) be the function defined by \(g(x)=\sqrt{\frac{\pi x}{2}=x^2}\).
- Let \(f:\R→\R\) be a function such that f(x + y) = f(x) + f(y) for all x, y ∈ \(\R\), and \(g:\R→(0,\infin)\) be a function such that g(x + y) = g(x)g(y) for all x, y ∈ \(\R\). If \(f(\frac{-3}{5})=12\) and \(g(\frac{-1}{3})=2\), then the value of \((f(\frac{1}{4})+g(-2)-8)g(0)\) is ______.
- Let \(f:\R→\R\) be a function defined by
\(f(x) = \begin{cases} x^2\sin(\frac{\pi}{x^2}), & \text{if } x \ne 0, \\ 0, & \text{if } x = 0. \end{cases}\)
Then which of the following statements is TRUE ?
Questions Asked in JEE Advanced exam
- A region in the form of an equilateral triangle (in x-y plane) of height L has a uniform magnetic field 𝐵⃗ pointing in the +z-direction. A conducting loop PQR, in the form of an equilateral triangle of the same height 𝐿, is placed in the x-y plane with its vertex P at x = 0 in the orientation shown in the figure. At 𝑡 = 0, the loop starts entering the region of the magnetic field with a uniform velocity 𝑣 along the +x-direction. The plane of the loop and its orientation remain unchanged throughout its motion.
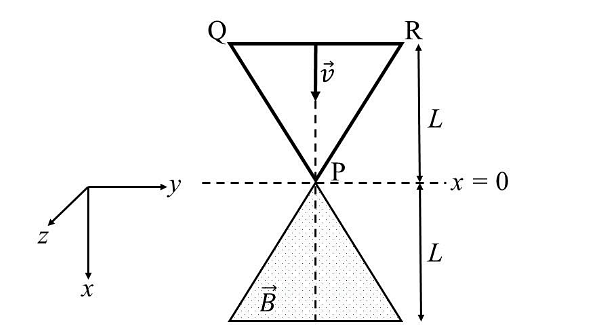
Which of the following graph best depicts the variation of the induced emf (E) in the loop as a function of the distance (𝑥) starting from 𝑥 = 0? - Two beads, each with charge q and mass m, are on a horizontal, frictionless, non-conducting, circular hoop of radius R. One of the beads is glued to the hoop at some point, while the other one performs small oscillations about its equilibrium position along the hoop. The square of the angular frequency of the small oscillations is given by [ \(\epsilon_0 \)is the permittivity of free space.]
- JEE Advanced - 2024
- Moving charges and magnetism
- A group of 9 students, s1, s2,…., s9, is to be divided to form three teams X, Y and Z of sizes 2, 3, and 4, respectively. Suppose that s1 cannot be selected for the team X and s2 cannot be selected for the team Y. Then the number of ways to form such teams, is _______.
- JEE Advanced - 2024
- Combinations
- Let \(\vec{p}=2\hat{i}+\hat{j}+3\hat{k}\) and \(\vec{q}=\hat{i}-\hat{j}+\hat{k}\). If for some real numbers α, β and γ we have
\(15\hat{i}+10\hat{j}+6\hat{k}=α(2\vec{p}+\vec{q})+β(\vec{p}-2\vec{q})+γ(\vec{p}\times\vec{q})\),
then the value of γ is ________.- JEE Advanced - 2024
- Vector Algebra
- Let X be a random variable, and let P(X = x) denote the probability that X takes the value x. Suppose that the points (x, P(X = x)), x = 0,1,2,3,4, lie on a fixed straight line in the xy -plane, and P(X = x) = 0 for all x ∈ R - {0,1,2,3,4}. If the mean of X is \(\frac{5}{2}\) , and the variance of X is α, then the value of 24α is ______.
- JEE Advanced - 2024
- Probability
Concepts Used:
Functions
A function is a relation between a set of inputs and a set of permissible outputs with the property that each input is related to exactly one output. Let A & B be any two non-empty sets, mapping from A to B will be a function only when every element in set A has one end only one image in set B.
Kinds of Functions
The different types of functions are -
One to One Function: When elements of set A have a separate component of set B, we can determine that it is a one-to-one function. Besides, you can also call it injective.
Many to One Function: As the name suggests, here more than two elements in set A are mapped with one element in set B.
Moreover, if it happens that all the elements in set B have pre-images in set A, it is called an onto function or surjective function.
Also, if a function is both one-to-one and onto function, it is known as a bijective. This means, that all the elements of A are mapped with separate elements in B, and A holds a pre-image of elements of B.
Read More: Relations and Functions



