Let $A (-3,2)$ and $B (-2,1)$ be the vertices of a triangle $ABC$. If the centroid of this triangle lies on the line $3x + 4y+2 = 0$, then the vertex $C$ lies on the line :
- $4x + 3y + 5 = 0$
- $3x + 4y + 3 = 0$
- $4x + 3y + 3 = 0$
- $3x + 4y + 5 = 0$
The Correct Option is B
Solution and Explanation
Centroid, E=$\left(\frac{x_{1}-5}{3}, \frac{y_{1}+3}{3}\right)$
Since centroid lies on the line
3x + 4y + 2 = 0
$\therefore\, 3\left(\frac{x_{1}-5}{3}\right) +4 \left(\frac{y_{1}+3}{3}\right)+2=0$
$\Rightarrow 3x_{1}+4y_{1}+3=0$
Hence vertex ($x_{1}, y_{1}$) lies on the line
$3x + 4y + 3 = 0$
Top Questions on Straight lines
- The vertices of a triangle are A(–1, 3), B(–2, 2) and C(3, –1). A new triangle is formed by shifting the sides of the triangle by one unit inwards. Then the equation of the side of the new triangle nearest to origin is :
- JEE Main - 2024
- Mathematics
- Straight lines
- If the sum of squares of all real values of \( \alpha \), for which the lines \( 2x - y + 3 = 0 \), \( 6x + 3y + 1 = 0 \) and \( \alpha x + 2y - 2 = 0 \) do not form a triangle \( p \), then the greatest integer less than or equal to \( p \) is ....
- JEE Main - 2024
- Mathematics
- Straight lines
- Which of the following cannot be the direction ratios of the straight line \(\frac{x - 3}{2} = \frac{2 - y}{3} = \frac{z + 4}{-1}\)?
- CUET (UG) - 2024
- Mathematics
- Straight lines
- A rectangle ABCD has its side parallel to the line y=2x and vertices A,B,D are on y=1,x=1 and x=-1 respectively. The coordinate of C can be
- WBJEE - 2023
- Mathematics
- Straight lines
- Ki are possible values of K for which lines \(Kx + 2y + 2 = 0\), \(2x + Ky + 3 = 0\), \(3x + 3y + K = 0\) are concurrent, then \(∑k_i\) has value.
- MHT CET - 2023
- Mathematics
- Straight lines
Questions Asked in JEE Main exam
- Let \[\vec{a} = \hat{i} + \hat{j} + \hat{k}, \quad \vec{b} = -\hat{i} - 8\hat{j} + 2\hat{k}, \quad \text{and} \quad \vec{c} = 4\hat{i} + c_2\hat{j} + c_3\hat{k} \]be three vectors such that \[\vec{b} \times \vec{a} = \vec{c} \times \vec{a}.\]If the angle between the vector $\vec{c}$ and the vector $3\hat{i} + 4\hat{j} + \hat{k}$ is $\theta$, then the greatest integer less than or equal to $\tan^2 \theta$ is:
- JEE Main - 2024
- Vector Algebra
- 10 mL of gaseous hydrocarbon on combustion gives 40 mL of CO\(_2\)(g) and 50 mL of water vapour. The total number of carbon and hydrogen atoms in the hydrocarbon is ______ .
- JEE Main - 2024
- Hydrocarbons
- If each term of a geometric progression \( a_1, a_2, a_3, \dots \) with \( a_1 = \frac{1}{8} \) and \( a_2 \neq a_1 \), is the arithmetic mean of the next two terms and \( S_n = a_1 + a_2 + \dots + a_n \), then \( S_{20} - S_{18} \) is equal to
- JEE Main - 2024
- Arithmetic Mean
A body of mass 1000 kg is moving horizontally with a velocity of 6 m/s. If 200 kg extra mass is added, the final velocity (in m/s) is:
- JEE Main - 2024
- speed and velocity
- $\textbf{Choose the correct statements about the hydrides of group 15 elements.}$
A. The stability of the hydrides decreases in the order \(\text{NH}_3 > \text{PH}_3 > \text{AsH}_3 > \text{SbH}_3 > \text{BiH}_3\)
B. The reducing ability of the hydrides increases in the order \(\text{NH}_3 < \text{PH}_3 < \text{AsH}_3 < \text{SbH}_3 < \text{BiH}_3\)
C. Among the hydrides, \(\text{NH}_3\) is a strong reducing agent while \(\text{BiH}_3\) is a mild reducing agent.
D. The basicity of the hydrides increases in the order \(\text{NH}_3 < \text{PH}_3 < \text{AsH}_3 < \text{SbH}_3 < \text{BiH}_3\)
Choose the most appropriate from the option given below:- JEE Main - 2024
- p -Block Elements
Concepts Used:
Straight lines
A straight line is a line having the shortest distance between two points.
A straight line can be represented as an equation in various forms, as show in the image below:
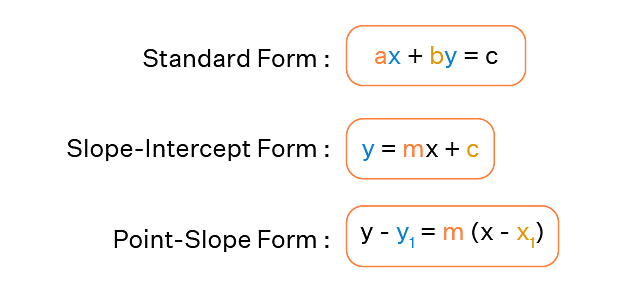
The following are the many forms of the equation of the line that are presented in straight line-
1. Slope – Point Form
Assume P0(x0, y0) is a fixed point on a non-vertical line L with m as its slope. If P (x, y) is an arbitrary point on L, then the point (x, y) lies on the line with slope m through the fixed point (x0, y0) if and only if its coordinates fulfil the equation below.
y – y0 = m (x – x0)
2. Two – Point Form
Let's look at the line. L crosses between two places. P1(x1, y1) and P2(x2, y2) are general points on L, while P (x, y) is a general point on L. As a result, the three points P1, P2, and P are collinear, and it becomes
The slope of P2P = The slope of P1P2 , i.e.
\(\frac{y-y_1}{x-x_1} = \frac{y_2-y_1}{x_2-x_1}\)
Hence, the equation becomes:
y - y1 =\( \frac{y_2-y_1}{x_2-x_1} (x-x1)\)
3. Slope-Intercept Form
Assume that a line L with slope m intersects the y-axis at a distance c from the origin, and that the distance c is referred to as the line L's y-intercept. As a result, the coordinates of the spot on the y-axis where the line intersects are (0, c). As a result, the slope of the line L is m, and it passes through a fixed point (0, c). The equation of the line L thus obtained from the slope – point form is given by
y – c =m( x - 0 )
As a result, the point (x, y) on the line with slope m and y-intercept c lies on the line, if and only if
y = m x +c



