Question:
In an interference arrangement similar to Young's
double-slit experiment, the slits $S_1$, and $S_2$ are illuminated
with coherent microwave sources, each of frequency $10^6$ Hz.
The sources are synchronized to have zero phase
difference. The slits are separated by a distance d = 150.0 m.
The intensity I$(\theta)$ is measured as a function of $\theta$, where $\theta$ is
defined as shown. If $I_0$ is the maximum intensity, then I$(\theta)$
for $0 \le \theta \le$90$^{\circ}$ is given by
In an interference arrangement similar to Young's
double-slit experiment, the slits $S_1$, and $S_2$ are illuminated
with coherent microwave sources, each of frequency $10^6$ Hz.
The sources are synchronized to have zero phase
difference. The slits are separated by a distance d = 150.0 m.
The intensity I$(\theta)$ is measured as a function of $\theta$, where $\theta$ is
defined as shown. If $I_0$ is the maximum intensity, then I$(\theta)$
for $0 \le \theta \le$90$^{\circ}$ is given by
Updated On: Jan 18, 2023
- $I (\theta)=I_0/2$ for $\theta$=30$^{\circ}$
- $I (\theta)=I_0/4$ for $\theta$=90$^{\circ}$
- $I (\theta)=I_0$ for $\theta$=0$^{\circ}$
- $I (\theta)$is constant for all values of $\theta$
Hide Solution
Verified By Collegedunia
The Correct Option is C
Solution and Explanation
The intensity of light is $I(\theta)=I_0 cos^2 \big(\frac{\delta}{2}\big)$
where, $\hspace20mm \delta=\frac{2 \pi}{\lambda}(\Delta x)$
$\hspace25mm =\big(\frac{2 \pi}{\lambda}\big)(d \, sin \, \theta)$
(a) For $\theta$ = 30$^{\circ}$
$ \, \, \, \, \lambda=\frac{c}{v}=\frac{3 \times 10^8}{10^6}=300 m$ and d = 150 m
$\hspace10mm \delta=\big(\frac{2 \pi}{300}\big)(150)\big(\frac{1}{2}\big)=\frac{\pi}{2}$
$\therefore \, \, \, \, \, \, \, \, \frac{\delta}{2}=\frac{\pi}{4}$
$\therefore \, \, \, \, \, \, \, I(\theta)=I_0 cos^2 \big(\frac{\pi}{4}\big)=\frac{I_0}{2} \hspace10mm$ [option (a)]
(b) For $\theta$=90$^{\circ}$
$\delta=\big(\frac{2 \pi}{300}\big)(150)(1)=\pi \, or \, \, \frac{\delta}{2}=\frac{\pi}{2} \, \, and \, \, I(\theta)=0$
(c) For $\theta=0^\circ,\delta=0 \, \, or \, \, \frac{\delta}{2}=0$
$\therefore I(\theta)=I_0 \hspace35mm$ [option (c)]
where, $\hspace20mm \delta=\frac{2 \pi}{\lambda}(\Delta x)$
$\hspace25mm =\big(\frac{2 \pi}{\lambda}\big)(d \, sin \, \theta)$
(a) For $\theta$ = 30$^{\circ}$
$ \, \, \, \, \lambda=\frac{c}{v}=\frac{3 \times 10^8}{10^6}=300 m$ and d = 150 m
$\hspace10mm \delta=\big(\frac{2 \pi}{300}\big)(150)\big(\frac{1}{2}\big)=\frac{\pi}{2}$
$\therefore \, \, \, \, \, \, \, \, \frac{\delta}{2}=\frac{\pi}{4}$
$\therefore \, \, \, \, \, \, \, I(\theta)=I_0 cos^2 \big(\frac{\pi}{4}\big)=\frac{I_0}{2} \hspace10mm$ [option (a)]
(b) For $\theta$=90$^{\circ}$
$\delta=\big(\frac{2 \pi}{300}\big)(150)(1)=\pi \, or \, \, \frac{\delta}{2}=\frac{\pi}{2} \, \, and \, \, I(\theta)=0$
(c) For $\theta=0^\circ,\delta=0 \, \, or \, \, \frac{\delta}{2}=0$
$\therefore I(\theta)=I_0 \hspace35mm$ [option (c)]
Was this answer helpful?
0
0
Top Questions on Youngs double slit experiment
- The maximum elongation of a steel wire of 1 m length if the elastic limit of steel and its Young’s modulus, respectively, are 8 × 108 N m–2 and 2 × 1011 N m–2, is :
- NEET (UG) - 2024
- Physics
- Youngs double slit experiment
- A metallic bar of Young’s modulus, 0.5 × 1011 N m–2 and coefficient of linear thermal expansion 10–5 °C–1, length 1 m and area of cross-section 10–3 m2 is heated from 0°C to 100°C without expansion or bending. The compressive force developed in it is :
- NEET (UG) - 2024
- Physics
- Youngs double slit experiment
- If the monochromatic source in Young's double slit experiment is replaced by white light, then coloured fringes. (3) there will be a central bright white fringe surrounded by a few coloured fringes. (4) all bright fringes will be of equal width.
- NEET (UG) - 2024
- Physics
- Youngs double slit experiment
- In a Young’s double slit experiment, each of the two slits A and B, as shown in the figure, are oscillating about their fixed center and with a mean separation of 0.8 mm. The distance between the slits at time t is given by 𝑑 = (0.8 + 0.04 sin 𝜔𝑡) mm, where 𝜔 = 0.08 rad s −1 . The distance of the screen from the slits is 1 m and the wavelength of the light used to illuminate the slits is 6000 Å. The interference pattern on the screen changes with time, while the central bright fringe (zeroth fringe) remains fixed at point O.
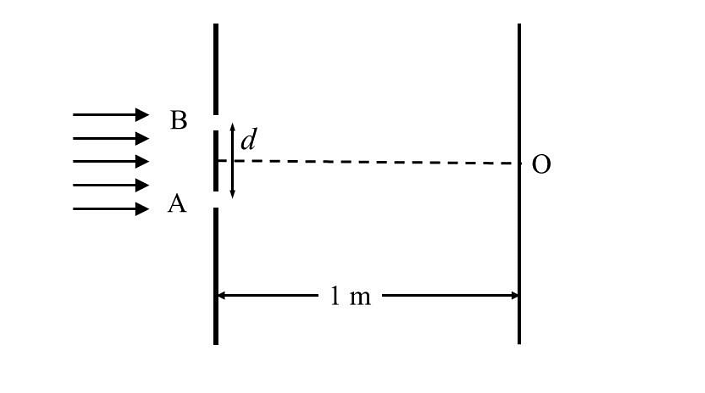
- JEE Advanced - 2024
- Physics
- Youngs double slit experiment
- If the area of cross-section is halved and length of a wire having Young's modulus Y is doubled, then its new Young's modulus will be
- JEE Main - 2024
- Physics
- Youngs double slit experiment
View More Questions
Questions Asked in JEE Advanced exam
- A region in the form of an equilateral triangle (in x-y plane) of height L has a uniform magnetic field 𝐵⃗ pointing in the +z-direction. A conducting loop PQR, in the form of an equilateral triangle of the same height 𝐿, is placed in the x-y plane with its vertex P at x = 0 in the orientation shown in the figure. At 𝑡 = 0, the loop starts entering the region of the magnetic field with a uniform velocity 𝑣 along the +x-direction. The plane of the loop and its orientation remain unchanged throughout its motion.
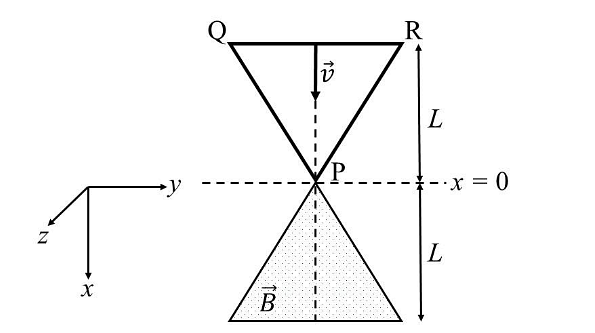
Which of the following graph best depicts the variation of the induced emf (E) in the loop as a function of the distance (𝑥) starting from 𝑥 = 0? - Two beads, each with charge q and mass m, are on a horizontal, frictionless, non-conducting, circular hoop of radius R. One of the beads is glued to the hoop at some point, while the other one performs small oscillations about its equilibrium position along the hoop. The square of the angular frequency of the small oscillations is given by [ \(\epsilon_0 \)is the permittivity of free space.]
- JEE Advanced - 2024
- Moving charges and magnetism
- A group of 9 students, s1, s2,…., s9, is to be divided to form three teams X, Y and Z of sizes 2, 3, and 4, respectively. Suppose that s1 cannot be selected for the team X and s2 cannot be selected for the team Y. Then the number of ways to form such teams, is _______.
- JEE Advanced - 2024
- Combinations
- Let \(\vec{p}=2\hat{i}+\hat{j}+3\hat{k}\) and \(\vec{q}=\hat{i}-\hat{j}+\hat{k}\). If for some real numbers α, β and γ we have
\(15\hat{i}+10\hat{j}+6\hat{k}=α(2\vec{p}+\vec{q})+β(\vec{p}-2\vec{q})+γ(\vec{p}\times\vec{q})\),
then the value of γ is ________.- JEE Advanced - 2024
- Vector Algebra
- Let X be a random variable, and let P(X = x) denote the probability that X takes the value x. Suppose that the points (x, P(X = x)), x = 0,1,2,3,4, lie on a fixed straight line in the xy -plane, and P(X = x) = 0 for all x ∈ R - {0,1,2,3,4}. If the mean of X is \(\frac{5}{2}\) , and the variance of X is α, then the value of 24α is ______.
- JEE Advanced - 2024
- Probability
View More Questions
Concepts Used:
Young’s Double Slit Experiment
- Considering two waves interfering at point P, having different distances. Consider a monochromatic light source ‘S’ kept at a relevant distance from two slits namely S1 and S2. S is at equal distance from S1 and S2. SO, we can assume that S1 and S2 are two coherent sources derived from S.
- The light passes through these slits and falls on the screen that is kept at the distance D from both the slits S1 and S2. It is considered that d is the separation between both the slits. The S1 is opened, S2 is closed and the screen opposite to the S1 is closed, but the screen opposite to S2 is illuminating.
- Thus, an interference pattern takes place when both the slits S1 and S2 are open. When the slit separation ‘d ‘and the screen distance D are kept unchanged, to reach point P the light waves from slits S1 and S2 must travel at different distances. It implies that there is a path difference in the Young double-slit experiment between the two slits S1 and S2.
Read More: Young’s Double Slit Experiment



