If $A = \frac{1}{3} \begin{bmatrix}1&2&2\\ 2&1&-2\\ a&2&b\end{bmatrix} $ is an orthogonal matrix, then
- a = - 2, b = - 1
- a = 2, b = 1
- a = 2, b = - 1
- a = - 2, b = 1
The Correct Option is A
Solution and Explanation
$\Rightarrow \frac{1}{3} \begin{bmatrix}1&2&2\\ 2&1&-2\\ a&2&b\end{bmatrix} . \frac{1}{3} \begin{bmatrix}1&2&a\\ 2&1&2\\ 2&-2&b\end{bmatrix} = \begin{bmatrix}1&0&0\\ 0&1&0\\ 0&0&1\end{bmatrix} $
$\Rightarrow \frac{1}{9} \begin{bmatrix}1&2&2\\ 2&1&-2\\ a&2&b\end{bmatrix} \begin{bmatrix}1&2&a\\ 2&1&2\\ 2&-2&b\end{bmatrix} = \begin{bmatrix}1&0&0\\ 0&1&0\\ 0&0&1\end{bmatrix} $
$\Rightarrow \begin{bmatrix}9&0&a+4+2b\\ 0&9&2a+2-2b\\ a+4+2b&2a+2-2b&a^{2}+4+b^{2}\end{bmatrix} = \begin{bmatrix}9&0&0\\ 0&9&0\\ 0&0&9\end{bmatrix} $
$\Rightarrow a + 4 + 2b = 0, 2a + 2 - 2b = 0 , a^{2} + 4 + b^{2} = 9 $
$\Rightarrow a + 2b + 4 = 0, a - b + 1 = 0 a^{2} + b^{2} = 5 $
$\Rightarrow a = - 2, b = - 1$
Top Questions on Transpose of a Matrix
- Let P be a square matrix such that P2 = I – P. For α, β, γ, δ ∈ N, if Pα + Pβ = γI – 29P and Pα – Pβ = δI – 13P, then α + β + γ – δ is equal to
- JEE Main - 2023
- Mathematics
- Transpose of a Matrix
- Let B =\(\begin{bmatrix} 1 & 3 & α \\ 1 & 2& 3 \\ α & α & 4 \end{bmatrix}\) , α>2 be the adjoint of a matrix A and |A| = 2, then [α - 2α α] B\(\begin{bmatrix} α \\ -2α \\ α \end{bmatrix}\)is equal to
- JEE Main - 2023
- Mathematics
- Transpose of a Matrix
- Given below are two statements: one is labelled as Assertion A and the other is labelled as Reason R.
Assertion A : For matrix A =\(\begin{bmatrix} 1 & 2 \\ 8 & 16 \end{bmatrix}\),rank of A = r(A) = 1
Reason R: For matrix A if |A| = 0, then it implies that rank of matrix A given by r(A) is less than full rank.
In the light of the above statements, choose the most appropriate answer from the options given below:- CUET (PG) - 2023
- Mathematics
- Transpose of a Matrix
- if A=\(\frac{1}{5! 6! 7!}\begin{bmatrix} 5! & 6! & 7!\\ 6! & 7! & 8! \\ 7! & 8! & 9! \end{bmatrix}\), then |adj(adj(2A))| is equal t
- JEE Main - 2023
- Mathematics
- Transpose of a Matrix
- Let Dk=\(\begin{vmatrix} 1 & 2k & 2k-1\\ n & n^2+n+2 & n^2 \\ n & n^2+n & n^2+n+2 \end{vmatrix} \) If \(∑^n_{k=1} D_k=96,\) The n is equal to
- JEE Main - 2023
- Mathematics
- Transpose of a Matrix
Questions Asked in BITSAT exam
- Two capacitors, of capacitance C, are connected in series. If one of them is filled with a dielectric substance K, what is the effective capacitance?
- BITSAT - 2023
- electrostatic potential and capacitance
- What is the dimension of the Gravitational constant?
- BITSAT - 2023
- Gravitation
- Minimum value of 5cos(2x) + 5sin(2x)
- BITSAT - 2023
- Trigonometric Functions
NaOH is deliquescent
- BITSAT - 2023
- States of matter
- The freezing point of the 0.05 molal solution of non - electrolyte in water is? (kf = 1.86)
- BITSAT - 2023
- Solutions
Concepts Used:
Transpose of a Matrix
The matrix acquired by interchanging the rows and columns of the parent matrix is called the Transpose matrix. The transpose matrix is also defined as - “A Matrix which is formed by transposing all the rows of a given matrix into columns and vice-versa.”
The transpose matrix of A is represented by A’. It can be better understood by the given example:

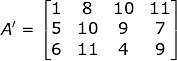
Now, in Matrix A, the number of rows was 4 and the number of columns was 3 but, on taking the transpose of A we acquired A’ having 3 rows and 4 columns. Consequently, the vertical Matrix gets converted into Horizontal Matrix.
Hence, we can say if the matrix before transposing was a vertical matrix, it will be transposed to a horizontal matrix and vice-versa.
Read More: Transpose of a Matrix



