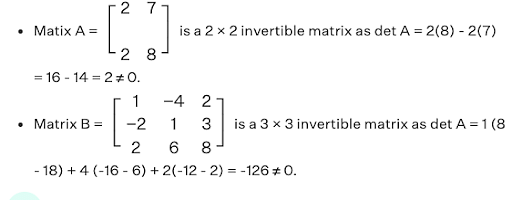Question:
If $A = \begin{bmatrix}2&-2\\ -2&2\end{bmatrix}$ then $A^n = 2^k A,$ where k =
If $A = \begin{bmatrix}2&-2\\ -2&2\end{bmatrix}$ then $A^n = 2^k A,$ where k =
Updated On: Jun 20, 2024
- $2^{n -1}$
- n + 1
- n - 1
- 2(n -1)
Hide Solution
Verified By Collegedunia
The Correct Option is D
Solution and Explanation
$A^{2} = \begin{bmatrix}2&-2\\ -2&2\end{bmatrix}\begin{bmatrix}2&-2\\ -2&2\end{bmatrix} =\begin{bmatrix}8&-8\\ -8&8\end{bmatrix} =4A = 2^{2}A $
$ A^{3} =A^{2} .A = 4A .A = 4 \left(4A\right) = 16A = 2^{4} A$
$ A^{4}= A^{3} .A = 16A.A= 16\left(4A\right) =64A=2^{6}A $
$ \therefore $ By inspection $k = 2(n - 1)$
$ A^{3} =A^{2} .A = 4A .A = 4 \left(4A\right) = 16A = 2^{4} A$
$ A^{4}= A^{3} .A = 16A.A= 16\left(4A\right) =64A=2^{6}A $
$ \therefore $ By inspection $k = 2(n - 1)$
Was this answer helpful?
4
6
Top Questions on Invertible Matrices
- If A is a non-identity invertible symmetric matrix, then \(A^{-1}\) is:
- CUET (UG) - 2023
- Mathematics
- Invertible Matrices
- The number of matrices of order 3 × 3, whose entries are either 0 or 1 and the sum of all the entries is a prime number, is _________.
- JEE Main - 2022
- Mathematics
- Invertible Matrices
- Which of the following matrices can NOT be obtained from the matrix \(\begin{bmatrix} -1 &2 \\ 1 & -1 \end{bmatrix}\) by a single elementary row operation?
- JEE Main - 2022
- Mathematics
- Invertible Matrices
- If A and B are invertible matrices then which of the following is not correct ?
- KCET - 2021
- Mathematics
- Invertible Matrices
- The inverse of the matrix $\begin{bmatrix}2&5&0\\ 0&1&1\\ -1&0&3\end{bmatrix} $ is
- KCET - 2019
- Mathematics
- Invertible Matrices
View More Questions
Questions Asked in KCET exam
- If \(\lim\limits_{x \rightarrow 0} \frac{\sin(2+x)-\sin(2-x)}{x}\)= A cos B, then the values of A and B respectively are
- KCET - 2023
- limits of trigonometric functions
- The Curie temperatures of Cobalt and iron are 1400K and 1000K respectively. At T = 1600K , the ratio of magnetic susceptibility of Cobalt to that of iron is
- KCET - 2023
- Magnetism and matter
- A particle is in uniform circular motion. Related to one complete revolution of the particle, which among the stataments is incorrect ?
- KCET - 2023
- Uniform Circular Motion
- The modulus of the complex number \(\frac{(1+i)^2(1+3i)}{(2-6i)(2-2i)}\) is
- KCET - 2023
- complex numbers
- The energy gap of an LED is 2.4 eV. When the LED is switched ‘ON’, the momentum of the emitted photons is
- KCET - 2023
- Semiconductor electronics: materials, devices and simple circuits
View More Questions
Concepts Used:
Invertible matrices
A matrix for which matrix inversion operation exists, given that it satisfies the requisite conditions is known as an invertible matrix. Any given square matrix A of order n × n is called invertible if and only if there exists, another n × n square matrix B such that, AB = BA = In, where In is an identity matrix of order n × n.
For example,
It can be observed that the determinant of the following matrices is non-zero.