Evaluate ∫cos2 xdx_________
Evaluate ∫cos2 xdx_________
-x/2+sin2x/4+c
x/2+sin2x/2+c
x/2+sin2x/4+c
-x/2+cos4x/4+c626d12d417cb86275feefcba
The Correct Option is A
Solution and Explanation
The correct option is (A): -x/2+sin2x/4+c
Top Questions on Integration by Parts
- \(∫xlog(1+x^2)dx=\)?
- KEAM - 2023
- Mathematics
- Integration by Parts
- If $\int\limits_0^1\left(x^{21}+x^{14}+x^7\right)\left(2 x^{14}+3 x^7+6\right)^{1 / 7} d x=\frac{1}{l}(11)^{m / n}$ where $l, m, n \in N , m$ and $n$ are coprime then $l+m+n$ is equal to ______
- JEE Main - 2023
- Mathematics
- Integration by Parts
- If \(f(x) + f(\pi-x) = \pi^{2}\) then \(_{0}\int^{\pi}f(x) sinx dx\) ?
- JEE Main - 2023
- Mathematics
- Integration by Parts
- \(∫_0^1 (5xe^{2x}-tan(π/4)) dx=\)
- KEAM - 2023
- Mathematics
- Integration by Parts
- If I=∫\(\frac{x^2dx}{(x\,sin\,x+cos\,x)^2}\)=f(x)+tan x+c, then f(x) is
- WBJEE - 2023
- Mathematics
- Integration by Parts
Questions Asked in SRMJEEE exam
The molar conductivities at infinite dilution for Na2SO4,K2S04,KCl, HCl and HCOONa at 300K are 260, 308, 150, 426, and 105 S cm2 mol-1, respectively. What will be A+m for formic acid in the same unit?
- SRMJEEE - 2023
- Electrochemistry
Which of the following statement is true for aqueous solution of 0.1 M urea, 0.2 M glucose nad 0.3 M sucrose
- SRMJEEE - 2023
- Biomolecules
Electrophilic halogenation of phenol does not require catalyst because
- SRMJEEE - 2023
- Haloalkanes and Haloarenes
- Which one is the correct expression of electric potential on the axial point of a dipole whose dipole moment is р and length is 2l, at a distance of r?
- SRMJEEE - 2023
- Electrostatics
- If VA and VVB are the potentials of the two points A and B, what will be the correct relation between the electric field and the potential difference between the points? The distance between the points is d.
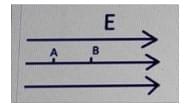
- SRMJEEE - 2023
- Electrostatics
Concepts Used:
Integration by Parts
Integration by Parts is a mode of integrating 2 functions, when they multiplied with each other. For two functions ‘u’ and ‘v’, the formula is as follows:
∫u v dx = u∫v dx −∫u' (∫v dx) dx
- u is the first function u(x)
- v is the second function v(x)
- u' is the derivative of the function u(x)
The first function ‘u’ is used in the following order (ILATE):
- 'I' : Inverse Trigonometric Functions
- ‘L’ : Logarithmic Functions
- ‘A’ : Algebraic Functions
- ‘T’ : Trigonometric Functions
- ‘E’ : Exponential Functions
The rule as a diagram:




