Consider a triangle $P Q R$ having sides of lengths $p, q$ and $r$ opposite to the angles $P, Q$ and $R$, respectively. Then which of the following statements is(are) TRUE?
- $\cos P \geq 1-\frac{ p ^{2}}{2 qr }$
- $\cos R \geq\left(\frac{q-r}{p+q}\right) \cos P+\left(\frac{p-r}{p+q}\right) \cos Q$
- $\frac{q+r}{p} < 2 \frac{\sqrt{\sin Q \sin R}}{\sin P}$
- If $p < q$ and $p < r$, then $\cos Q >\frac{ p }{ r }$ and $\cos R >\frac{ p }{ q }$
The Correct Option is A, B
Solution and Explanation
(A) \(\cos P = \frac{{q^2 + r^2 - p^2}}{{2qr}}\)
And \(\frac{{q^2 + r^2}}{2} \geq \sqrt{q^2 \cdot r^2} \quad \text{(AM} \geq \text{GM)}\)
\(⇒\) \(q^2 + r^2 \geq 2qr\)
So \(\cos P \geq \frac{{2qr - p^2}}{{2qr}}\)
\(\cos P \geq 1 - \frac{{p^2}}{{2qr}}\)
(B) \(\frac{{(q-r) \cos P + (p-r) \cos Q}}{{p+q}} = \frac{{(q \cos P + p \cos Q) - r(\cos P + \cos Q)}}{{p+q}}\)
=\(\frac{r(1 - \cos P - \cos Q)}{p+q}\)
=\(\frac{{r(q-p \cos R) - (p-q \cos R)}}{{p+q}}\)
= \(\frac{{(r-p-q) + (p+q)\cos R}}{{p+q}}\)
= \(\cos R + \frac{{r-q-p}}{{p+q}} \leq \cos R\)
(C) \(\frac{{q+r}}{p} = \frac{{\sin Q + \sin R}}{{\sin P}} \geq 2\sqrt{\frac{{\sin Q \sin R}}{{\sin P}}}\)
(D) If \(p < q \quad \text{and} \quad q < r\)
So, p is the smallest side, therefore one of Q or R can be obtuse
So, one of cos Q or cos R can be negative
Therefore, \(\cos Q > \frac{p}{r} \quad \text{and} \quad \cos R > \frac{p}{q} \text{ cannot hold always.}\)
Top Questions on Some Applications of Trigonometry
- If \(4 cos\ θ + 5 sin\ θ = 1\), then all possible values of \(tan\ θ\), is/are
Where, \(θ∈(-\frac \pi2,\frac \pi2)\)- JEE Main - 2024
- Mathematics
- Some Applications of Trigonometry
- If \(\frac {3cos\ 2x+cos^32x}{cos^6x-sin^6x}=x^3-x^2+6\), then find sum of roots.
- JEE Main - 2024
- Mathematics
- Some Applications of Trigonometry
Height of tower AB is 30 m where B is foot of tower. Angle of elevation from a point C on level ground to top of tower is 60° and angle of elevation of A from a point D x m above C is 15° then find the area of quadrilateral ABCD.
- JEE Main - 2023
- Mathematics
- Some Applications of Trigonometry
Let \(\alpha\ and\ \beta\) be real numbers such that \(-\frac{\pi}{4}<\beta<0<\alpha<\frac{\pi}{4}\). If \(\sin (\alpha+\beta)=\frac{1}{3}\ and\ \cos (\alpha-\beta)=\frac{2}{3}\), then the greatest integer less than or equal to
\(\left(\frac{\sin \alpha}{\cos \beta}+\frac{\cos \beta}{\sin \alpha}+\frac{\cos \alpha}{\sin \beta}+\frac{\sin \beta}{\cos \alpha}\right)^2\) is ____- JEE Advanced - 2023
- Mathematics
- Some Applications of Trigonometry
- A horizontal park is in the shape of a triangle OAB with AB = 16. A vertical lamp post OP is erected at the point O such that\( \begin{array}{l}\angle PAO = \angle PBO = 15^\circ ~\text{and}~ \angle PCO = 45^\circ,\end{array}\)where C is the midpoint of AB. Then (OP)2 is equal to
- JEE Main - 2022
- Mathematics
- Some Applications of Trigonometry
Questions Asked in JEE Advanced exam
- Let \(S=\left\{\begin{pmatrix} 0 & 1 & c \\ 1 & a & d\\ 1 & b & e \end{pmatrix}:a,b,c,d,e\in\left\{0,1\right\}\ \text{and} |A|\in \left\{-1,1\right\}\right\}\), where |A| denotes the determinant of A. Then the number of elements in S is _______.
- JEE Advanced - 2024
- Matrices
- A block of mass \(5 kg\) moves along the \(x-\)direction subject to the force \(F = (−20x + 10) N,\) with the value of \(x \) in metre. At time \(t = 0 s,\) it is at rest at position \(x = 1 m\). The position and momentum of the block at \(t = (\pi/4)\) s are
- JEE Advanced - 2024
- Work-energy theorem
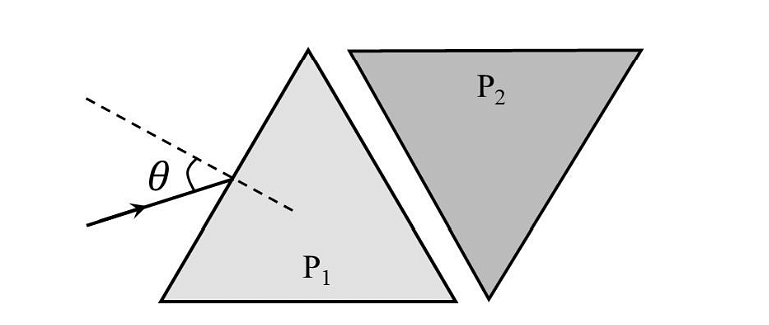
- Two equilateral-triangular prisms \(P_1 \)and \(P_2\) are kept with their sides parallel to each other, in vacuum, as shown in the figure. A light ray enters prism \(P_1\) at an angle of incidence 𝜃 such that the outgoing ray undergoes minimum deviation in prism \(P_2\). If the respective refractive indices of \(P_1\) and\( P_2\) are \(√ 3 /2\) and \(√3\), then \(\theta = sin{−1}[\sqrt \frac{ 3}{ 2} sin ( \frac{\pi}{B} )],\) where the value of \(\beta\) is ______.
- JEE Advanced - 2024
- Ray optics and optical instruments
- Let \(\overrightarrow{OP}=\frac{\alpha-1}{\alpha}\hat{i}+\hat{j}+\hat{k},\overrightarrow{OQ}=\hat{i}+\frac{\beta-1}{\beta}\hat{j}+\hat{k}\) and \(\overrightarrow{OR}=\hat{i}+\hat{j}+\frac{1}{2}\hat{k}\) be three vector where α, β ∈ R - {0} and 0 denotes the origin. If \((\overrightarrow{OP}\times\overrightarrow{OQ}).\overrightarrow{OR}=0\) and the point (α, β, 2) lies on the plane 3x + 3y - z + l = 0, then the value of l is _______.
- JEE Advanced - 2024
- Vector Algebra
- Let \(\vec{p}=2\hat{i}+\hat{j}+3\hat{k}\) and \(\vec{q}=\hat{i}-\hat{j}+\hat{k}\). If for some real numbers α, β and γ we have
\(15\hat{i}+10\hat{j}+6\hat{k}=α(2\vec{p}+\vec{q})+β(\vec{p}-2\vec{q})+γ(\vec{p}\times\vec{q})\),
then the value of γ is ________.- JEE Advanced - 2024
- Vector Algebra
JEE Advanced Notification
 JCECEB has released Seat Matrix of Online Counselling, Check HereSep 19, 2024
JCECEB has released Seat Matrix of Online Counselling, Check HereSep 19, 2024


