Question:
A spherical drop of capacitance $1 \mu \,F$ is broken into eight drops of equal radius. Then, the capacitance of each small drop is ........
A spherical drop of capacitance $1 \mu \,F$ is broken into eight drops of equal radius. Then, the capacitance of each small drop is ........
Updated On: Apr 15, 2024
- $\frac{1}{8}\,\mu F$
- $8\,\mu F$
- $\frac{1}{2}\,\mu F$
- $\frac{1}{4}\,\mu F$
Hide Solution
Verified By Collegedunia
The Correct Option is C
Solution and Explanation
Potential of a charged sphere is given by the formula
$V =\frac{ kQ }{ R }$
Hence, by $Q = CV$,
$C =\frac{ Q }{ V }=\frac{ R }{ k }$
As per given information, $\frac{ R }{ k }=1 \mu F$
After splitting,
$8\left(\frac{4}{3} \pi r ^{3}\right)=\frac{4}{3} \pi R ^{3}$
$r =\frac{ R }{2}$
Thus, capacitance of each small drop is $V =\frac{ r }{ k }=\frac{1}{2} \frac{ R }{ k }=\frac{1}{2} \mu F$
$V =\frac{ kQ }{ R }$
Hence, by $Q = CV$,
$C =\frac{ Q }{ V }=\frac{ R }{ k }$
As per given information, $\frac{ R }{ k }=1 \mu F$
After splitting,
$8\left(\frac{4}{3} \pi r ^{3}\right)=\frac{4}{3} \pi R ^{3}$
$r =\frac{ R }{2}$
Thus, capacitance of each small drop is $V =\frac{ r }{ k }=\frac{1}{2} \frac{ R }{ k }=\frac{1}{2} \mu F$
Was this answer helpful?
0
0
Top Questions on electrostatic potential and capacitance
An electric charge \(10^{-6} \, \mu C\) is placed at the origin (0, 0) of an X-Y coordinate system. Two points P and Q are situated at \((\sqrt{3}, \sqrt{3}) \, \text{mm}\) and \((\sqrt{6}, 0) \, \text{mm}\) respectively. The potential difference between the points P and Q will be:
- JEE Main - 2024
- Physics
- electrostatic potential and capacitance
- An infinitely long thin wire, having a uniform charge density per unit length of \(5 nC/m,\) is passing through a spherical shell of radius \(1 m\), as shown in the figure. A \(10 nC\) charge is distributed uniformly over the spherical shell. If the configuration of the charges remains static, the magnitude of the potential difference between points P and R, in Volt, is ______. [Given: In SI units \(\frac{1}{ 4πϵ0} = 9 × 10^9 , ln \ 2 = 0.7\). Ignore the area pierced by the wire.]
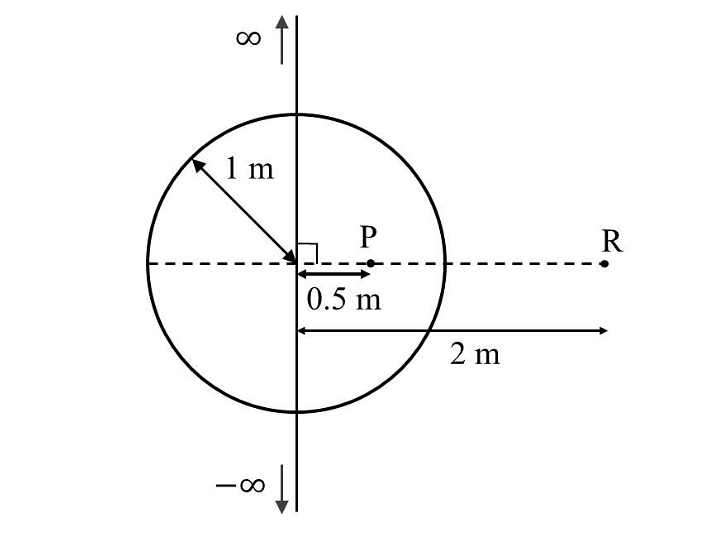
- JEE Advanced - 2024
- Physics
- electrostatic potential and capacitance
- Two capacitors, of capacitance C, are connected in series. If one of them is filled with a dielectric substance K, what is the effective capacitance?
- BITSAT - 2023
- Physics
- electrostatic potential and capacitance
- A parallel plate capacitor with plate area A and plate separation d is filed with a dielectric material of dielectric constant K = 4. The thickness of the dielectric material is x, where \(x < d\).

Let C1 and C2 be the capacitance of the system for \(x=\frac{1}{3d}\) and \(x=\frac{2d}{3}\), respectively. If \(C_1 = 2μF\), the value of C2 is __________μF.- JEE Main - 2023
- Physics
- electrostatic potential and capacitance
- An electric dipole is placed as shown in the figure.
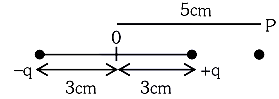
- NEET (UG) - 2023
- Physics
- electrostatic potential and capacitance
View More Questions
Questions Asked in KCET exam
- If \(\lim\limits_{x \rightarrow 0} \frac{\sin(2+x)-\sin(2-x)}{x}\)= A cos B, then the values of A and B respectively are
- KCET - 2023
- limits of trigonometric functions
- The Curie temperatures of Cobalt and iron are 1400K and 1000K respectively. At T = 1600K , the ratio of magnetic susceptibility of Cobalt to that of iron is
- KCET - 2023
- Magnetism and matter
- A particle is in uniform circular motion. Related to one complete revolution of the particle, which among the stataments is incorrect ?
- KCET - 2023
- Uniform Circular Motion
- The modulus of the complex number \(\frac{(1+i)^2(1+3i)}{(2-6i)(2-2i)}\) is
- KCET - 2023
- complex numbers
- The energy gap of an LED is 2.4 eV. When the LED is switched ‘ON’, the momentum of the emitted photons is
- KCET - 2023
- Semiconductor electronics: materials, devices and simple circuits
View More Questions



