A point mass is subjected to two simultaneous sinusoidal
displacements in x-direction, $ x_1 (t) = A sin \omega t $ and
$x_2(t) = Asin\bigg( \omega t + \frac{ 2 \pi }{ 3} \bigg) $ Adding a third sinusoidal
displacement $x_3(t)=B sin(\omega l + \Phi) $ brings the mass to a
complete rest. The values of B and $\Phi $ are
- $\sqrt 2 A , \frac{ 3 \pi }{4}$
- $ A , \frac{ 4 \pi }{3}$
- $\sqrt 3 A , \frac{ 5 \pi }{6}$
- $ A , \frac{ \pi }{3}$
The Correct Option is B
Solution and Explanation
To make resultant of $ x_1 ,x_2 \, \, and \, \, x_3 $ to be zero.$ A_3 $ should be
equal to A at angle $ \Phi =\frac{4 \pi }{3} $ as shown in figure.
$\therefore $ Correct answer is (b).
$ \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, $
Alternate Solution
It we substitute, $x_1 +x_2 + x_3 =0 $
or $ Asin \omega t + A sin \bigg( \omega t + \frac{ 2 \pi}{3} \bigg) + B sin (\omega t + \Phi ) =0 $
Then by applying simple mathematics we can prove that
$ B= A \, \, and \, \, \Phi = \frac{ 4 \pi}{3}$
Top Questions on Oscillations
- A particle is doing simple harmonic motion of amplitude 0.06 m and time period 3.14 s. The maximum velocity of the particle is _______ cm/s.
- JEE Main - 2024
- Physics
- Oscillations
- An object of mass \( 0.2 \, \text{kg} \) executes simple harmonic motion along the \( x \)-axis with a frequency of \( \left( \frac{25}{\pi} \right) \, \text{Hz} \). At the position \( x = 0.04 \, \text{m} \), the object has kinetic energy \( 0.5 \, \text{J} \) and potential energy \( 0.4 \, \text{J} \). The amplitude of oscillation is \(\dots\) \(\text{cm}\).
- JEE Main - 2024
- Physics
- Oscillations
- A particle performs simple harmonic motion with amplitude \( A \). Its speed is increased to three times at an instant when its displacement is \( \frac{2A}{3} \). The new amplitude of motion is \( \frac{nA}{3} \). The value of \( n \) is _____.
- JEE Main - 2024
- Physics
- Oscillations
- A tuning fork resonates with a sonometer wire of length 1 m stretched with a tension of 6 N. When the tension in the wire is changed to 54 N, the same tuning fork produces 12 beats per second with it. The frequency of the tuning fork is _______ Hz.
- JEE Main - 2024
- Physics
- Oscillations
- A particle executes simple harmonic motion with an amplitude of 4 cm. At the mean position, the velocity of the particle is 10 cm/s. The distance of the particle from the mean position when its speed becomes 5 cm/s is \( \sqrt{\alpha} \) cm, where $\alpha$ = ______
- JEE Main - 2024
- Physics
- Oscillations
Questions Asked in JEE Advanced exam
- A closed vessel contains 10 g of an ideal gas X at 300 K, which exerts 2 atm pressure. At the same temperature, 80 g of another ideal gas Y is added to it and the pressure becomes 6 atm. The ratio of root mean square velocities of X and Y at 300 K is
- JEE Advanced - 2024
- States of matter
- Let the function \(f:[1,\infin)→\R\) be defined by
\(f(t) = \begin{cases} (-1)^{n+1}2, & \text{if } t=2n-1,n\in\N, \\ \frac{(2n+1-t)}{2}f(2n-1)+\frac{(t-(2n-1))}{2}f(2n+1) & \text{if } 2n-1<t<2n+1,n\in\N. \end{cases}\)
Define \(g(x)=\int\limits_{1}^{x}f(t)dt,x\in(1,\infin).\) Let α denote the number of solutions of the equation g(x) = 0 in the interval (1, 8] and \(β=\lim\limits_{x→1+}\frac{g(x)}{x-1}\). Then the value of α + β is equal to _____.- JEE Advanced - 2024
- Integral Calculus
- A dimensionless quantity is constructed in terms of electronic charge \(e\), permittivity of free space \(\epsilon_0\) , Planck’s constant ℎ, and speed of light c. If the dimensionless quantity is written as \(e^\alpha\epsilon_0^\beta h^\gamma c^\delta\)and n is a non-zero integer, then\((\alpha, \beta,\gamma,\delta)\) is given by
- JEE Advanced - 2024
- Semiconductor electronics: materials, devices and simple circuits
- A block of mass \(5 kg\) moves along the \(x-\)direction subject to the force \(F = (−20x + 10) N,\) with the value of \(x \) in metre. At time \(t = 0 s,\) it is at rest at position \(x = 1 m\). The position and momentum of the block at \(t = (\pi/4)\) s are
- JEE Advanced - 2024
- Work-energy theorem
- A region in the form of an equilateral triangle (in x-y plane) of height L has a uniform magnetic field 𝐵⃗ pointing in the +z-direction. A conducting loop PQR, in the form of an equilateral triangle of the same height 𝐿, is placed in the x-y plane with its vertex P at x = 0 in the orientation shown in the figure. At 𝑡 = 0, the loop starts entering the region of the magnetic field with a uniform velocity 𝑣 along the +x-direction. The plane of the loop and its orientation remain unchanged throughout its motion.
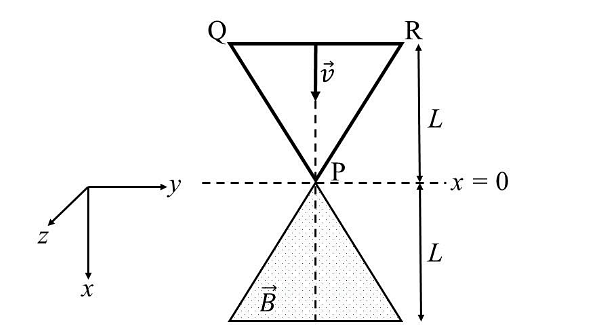
Which of the following graph best depicts the variation of the induced emf (E) in the loop as a function of the distance (𝑥) starting from 𝑥 = 0?
Concepts Used:
Oscillations
Oscillation is a process of repeating variations of any quantity or measure from its equilibrium value in time . Another definition of oscillation is a periodic variation of a matter between two values or about its central value.
The term vibration is used to describe the mechanical oscillations of an object. However, oscillations also occur in dynamic systems or more accurately in every field of science. Even our heartbeats also creates oscillations. Meanwhile, objects that move to and fro from its equilibrium position are known as oscillators.
Read More: Simple Harmonic Motion
Oscillation- Examples
The tides in the sea and the movement of a simple pendulum of the clock are some of the most common examples of oscillations. Some of examples of oscillations are vibrations caused by the guitar strings or the other instruments having strings are also and etc. The movements caused by oscillations are known as oscillating movements. For example, oscillating movements in a sine wave or a spring when it moves up and down.
The maximum distance covered while taking oscillations is known as the amplitude. The time taken to complete one cycle is known as the time period of the oscillation. The number of oscillating cycles completed in one second is referred to as the frequency which is the reciprocal of the time period.



