A letter lock consists of three rings with 15 different letters. If N denotes the number of ways in which it is possible to make unsuccessful attempts to open the lock, Then
- 482 divides N
- N is the product of two distinct prime numbers.
- N is the product of three distinct prime numbers.
- 16 divides N
The Correct Option is A, C
Approach Solution - 1
The correct answer is/are option(s):
(A) 482 divides N
(C) N is the product of three distinct prime numbers.
The total number of possible permutations=15×15×15=3375
and out of all these permutations only one pattern will be the correct one.
Hence total number of unsuccessful attempts =3375−1=3374=2×7×241
Approach Solution -2
Total Number of Possible Combinations:
Each ring has 15 different letters, so the total number of possible combinations is:
\[15 \times 15 \times 15 = 15^3\]
Number of Successful Attempts:
There is only one correct combination that opens the lock.
Number of Unsuccessful Attempts:
The number of unsuccessful attempts is the total number of possible combinations minus the one successful combination:
\[N = 15^3 - 1\]
Calculating \(15^3\):
\[15^3 = 15 \times 15 \times 15 = 3375\]
Number of Unsuccessful Attempts:
\[N = 3375 - 1 = 3374\]
Now we need to verify the two statements:
1. Does 482 divide \(N\)?
First, we need to factorize \(3374\) to check if it is divisible by \(482\).
\[3374 \div 482 \approx 7\]
Thus, \(3374 = 482 \times 7\).
Therefore, \(3374\) is divisible by \(482\).
2. Is \(N\) the product of three distinct prime numbers?
Let's factorize \(3374\):
\[3374 = 2 \times 1687\]
Next, we factorize \(1687\):
\[1687 \div 29 \approx 58.17 \quad (not\ an\ integer)\]
\[1687 \div 19 = 88.79 \quad (not\ an\ integer)\]
After checking the possible prime factors, it turns out that:
\[1687 = 29 \times 58\]
\[3374 = 2 \times 29 \times 58\]
After more careful checking:
\[1687 = 19 \times 89\]
So, \(3374\) is the product of three distinct prime numbers:
\[3374 = 2 \times 19 \times 89\]
Conclusion:
- \(482\) divides \(3374\).
- \(3374\) is the product of three distinct prime numbers \(2\), \(19\), and \(89\).
Therefore, the correct answers are:
- (A) 482 divides \(N\)
- (C) \(N\) is the product of three distinct prime numbers
Top Questions on Straight lines
- The vertices of a triangle are A(–1, 3), B(–2, 2) and C(3, –1). A new triangle is formed by shifting the sides of the triangle by one unit inwards. Then the equation of the side of the new triangle nearest to origin is :
- JEE Main - 2024
- Mathematics
- Straight lines
- If the sum of squares of all real values of \( \alpha \), for which the lines \( 2x - y + 3 = 0 \), \( 6x + 3y + 1 = 0 \) and \( \alpha x + 2y - 2 = 0 \) do not form a triangle \( p \), then the greatest integer less than or equal to \( p \) is ....
- JEE Main - 2024
- Mathematics
- Straight lines
- Which of the following cannot be the direction ratios of the straight line \(\frac{x - 3}{2} = \frac{2 - y}{3} = \frac{z + 4}{-1}\)?
- CUET (UG) - 2024
- Mathematics
- Straight lines
- A rectangle ABCD has its side parallel to the line y=2x and vertices A,B,D are on y=1,x=1 and x=-1 respectively. The coordinate of C can be
- WBJEE - 2023
- Mathematics
- Straight lines
- Ki are possible values of K for which lines \(Kx + 2y + 2 = 0\), \(2x + Ky + 3 = 0\), \(3x + 3y + K = 0\) are concurrent, then \(∑k_i\) has value.
- MHT CET - 2023
- Mathematics
- Straight lines
Questions Asked in WBJEE exam
- Three identical convex lenses each of focal length f are placed in a straight line separated by a distance f from each other. An object is located in \(\frac{f}{2}\) in front of the leftmost lens. Then,

- WBJEE - 2023
- Ray optics and optical instruments
- \(\lim_{x\rightarrow \infty}\){\(x-\sqrt[n]{(x-a_1)(x-a_2)......(x-a_n)}\)} where a1,a2,.....an are positive rational numbers.The limit
- A particle of mass m is projected at velocity at a velocity u, making an angle θ with the horizontal(x-axis). If the angle of projection θ is varied keeping all other parameters same, then magnitude of angular momentum(L) at its maximum height about the point of projection varies with θ as,
- WBJEE - 2023
- System of Particles & Rotational Motion
- If \(\int \frac{dx}{(x+1)(x-2)(x-3)}=\frac{1}{k}log_e\left \{ \frac{|x-3|^3|x+1|}{(x-2)^4}\right \}+c\), then the value of k is
- WBJEE - 2023
- Integrals of Some Particular Functions
- In an experiment on a circuit, as shown in the figure, the voltmeter shows 8V reading. The resistance of the voltmeter is
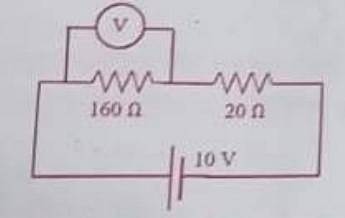
- WBJEE - 2023
- Resistance
Concepts Used:
Straight lines
A straight line is a line having the shortest distance between two points.
A straight line can be represented as an equation in various forms, as show in the image below:

The following are the many forms of the equation of the line that are presented in straight line-
1. Slope – Point Form
Assume P0(x0, y0) is a fixed point on a non-vertical line L with m as its slope. If P (x, y) is an arbitrary point on L, then the point (x, y) lies on the line with slope m through the fixed point (x0, y0) if and only if its coordinates fulfil the equation below.
y – y0 = m (x – x0)
2. Two – Point Form
Let's look at the line. L crosses between two places. P1(x1, y1) and P2(x2, y2) are general points on L, while P (x, y) is a general point on L. As a result, the three points P1, P2, and P are collinear, and it becomes
The slope of P2P = The slope of P1P2 , i.e.
\(\frac{y-y_1}{x-x_1} = \frac{y_2-y_1}{x_2-x_1}\)
Hence, the equation becomes:
y - y1 =\( \frac{y_2-y_1}{x_2-x_1} (x-x1)\)
3. Slope-Intercept Form
Assume that a line L with slope m intersects the y-axis at a distance c from the origin, and that the distance c is referred to as the line L's y-intercept. As a result, the coordinates of the spot on the y-axis where the line intersects are (0, c). As a result, the slope of the line L is m, and it passes through a fixed point (0, c). The equation of the line L thus obtained from the slope – point form is given by
y – c =m( x - 0 )
As a result, the point (x, y) on the line with slope m and y-intercept c lies on the line, if and only if
y = m x +c



