A length-scale $(\ell)$ depends on the permittivity $(\varepsilon)$ of a dielectric material, Boltzmann constant $\left( k _{ B }\right)$, the absolute temperature $(T)$, the number per unit volume $(n)$ of certain charged particles, and the charge $(q)$ carried by each of the particles. Which of the following expressions (s) for $\ell$ is (are) dimensionally correct?
- $\ell=\sqrt{\left(\frac{ nq ^{2}}{\varepsilon k _{ B } T }\right)}$
- $\ell=\sqrt{\left(\frac{\varepsilon k _{ B } T }{ nq ^{2}}\right)}$
- $\ell=\sqrt{\left(\frac{q^{2}}{\varepsilon n^{2 / 3} k_{B} T}\right)}$
- $\ell=\sqrt{\left(\frac{q^{2}}{\operatorname{sn}^{1 / 3} k_{B} T}\right)}$
The Correct Option is D
Solution and Explanation
\(\ell \alpha \varepsilon^{a} k ^{ b } T ^{ c } n ^{ d } q ^{ e }\)
(A) \(\ell=\sqrt{\frac{L^{-3} \times A^{2} T^{2}}{M^{-1} A^{2} T^{4} L^{-3} M^{1} L^{2} T^{-2} \theta^{-1} \theta}}\)
\(\ell=\sqrt{\frac{1}{L^{2}}}=\frac{1}{L}\)
(B) \(\ell =\sqrt{\frac{\varepsilon k_{B} T}{n q^{2}}}\)
\(=\sqrt{\frac{\left(M^{-1} A^{2} T^{4} L^{-3}\right) M^{1} L^{2} T^{-2} \theta^{-1} \theta}{L^{-3} A^{1} T^{2}}}\)
\(=\sqrt{L^{2}}=L\)
(C) \(\ell=\sqrt{\frac{A^{2} T^{2}}{M^{-1} A^{2} T^{4} L^{-3} L^{-2} M^{1} L^{2} T^{-2} \theta^{-1} \theta}}\)
(D) \(\ell=\sqrt{\frac{ A ^{2} T ^{2}}{ M ^{-1} A ^{2} T ^{4} L^{-3} L ^{-1} M ^{+1} L ^{2} T ^{-2} \theta^{-1} \theta}}\)
\(=\sqrt{L^{2}}= L\)
So, the correct option is (D): \(\ell=\sqrt{\left(\frac{q^{2}}{\operatorname{sn}^{1 / 3} k_{B} T}\right)}\)
Top Questions on Dimensional Analysis
- The dimensions of angular impulse is equal to :
- JEE Main - 2024
- Physics
- Dimensional Analysis
- If $R , X _{ L }$, and $X _{ C }$ represent resistance, inductive reactance and capacitive reactance Then which of the following is dimensionless :
- JEE Main - 2023
- Physics
- Dimensional Analysis
- If the velocity of light $c$, universal gravitational constant $G$ and Planck's constant $h$ are chosen as fundamental quantities The dimensions of mass in the new system is :
- JEE Main - 2023
- Physics
- Dimensional Analysis
- Identify the pair of physical quantities which have different dimensions.
- JEE Main - 2022
- Physics
- Dimensional Analysis
Velocity (v) and acceleration (a) in two systems of units 1 and 2 are related as
\(v_2=\frac{n}{m^2}v_1\) and \(a_2=\frac{a_1}{mn}\)
respectively. Here m and n are constants. The relations for distance and time in two systems respectively are :- JEE Main - 2022
- Physics
- Dimensional Analysis
Questions Asked in JEE Advanced exam
- Let \(S=\left\{\begin{pmatrix} 0 & 1 & c \\ 1 & a & d\\ 1 & b & e \end{pmatrix}:a,b,c,d,e\in\left\{0,1\right\}\ \text{and} |A|\in \left\{-1,1\right\}\right\}\), where |A| denotes the determinant of A. Then the number of elements in S is _______.
- JEE Advanced - 2024
- Matrices
- A block of mass \(5 kg\) moves along the \(x-\)direction subject to the force \(F = (−20x + 10) N,\) with the value of \(x \) in metre. At time \(t = 0 s,\) it is at rest at position \(x = 1 m\). The position and momentum of the block at \(t = (\pi/4)\) s are
- JEE Advanced - 2024
- Work-energy theorem
- Two equilateral-triangular prisms \(P_1 \)and \(P_2\) are kept with their sides parallel to each other, in vacuum, as shown in the figure. A light ray enters prism \(P_1\) at an angle of incidence 𝜃 such that the outgoing ray undergoes minimum deviation in prism \(P_2\). If the respective refractive indices of \(P_1\) and\( P_2\) are \(√ 3 /2\) and \(√3\), then \(\theta = sin{−1}[\sqrt \frac{ 3}{ 2} sin ( \frac{\pi}{B} )],\) where the value of \(\beta\) is ______.
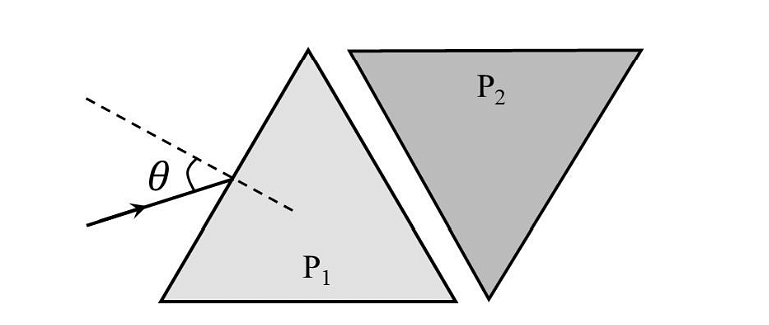
- JEE Advanced - 2024
- Ray optics and optical instruments
- Let \(\overrightarrow{OP}=\frac{\alpha-1}{\alpha}\hat{i}+\hat{j}+\hat{k},\overrightarrow{OQ}=\hat{i}+\frac{\beta-1}{\beta}\hat{j}+\hat{k}\) and \(\overrightarrow{OR}=\hat{i}+\hat{j}+\frac{1}{2}\hat{k}\) be three vector where α, β ∈ R - {0} and 0 denotes the origin. If \((\overrightarrow{OP}\times\overrightarrow{OQ}).\overrightarrow{OR}=0\) and the point (α, β, 2) lies on the plane 3x + 3y - z + l = 0, then the value of l is _______.
- JEE Advanced - 2024
- Vector Algebra
- Let \(\vec{p}=2\hat{i}+\hat{j}+3\hat{k}\) and \(\vec{q}=\hat{i}-\hat{j}+\hat{k}\). If for some real numbers α, β and γ we have
\(15\hat{i}+10\hat{j}+6\hat{k}=α(2\vec{p}+\vec{q})+β(\vec{p}-2\vec{q})+γ(\vec{p}\times\vec{q})\),
then the value of γ is ________.- JEE Advanced - 2024
- Vector Algebra
Concepts Used:
Dimensional Analysis
Dimensional Analysis is a process which helps verify any formula by the using the principle of homogeneity. Basically dimensions of each term of a dimensional equation on both sides should be the same.
Limitation of Dimensional Analysis: Dimensional analysis does not check for the correctness of value of constants in an equation.
Using Dimensional Analysis to check the correctness of the equation
Let us understand this with an example:
Suppose we don’t know the correct formula relation between speed, distance and time,
We don’t know whether
(i) Speed = Distance/Time is correct or
(ii) Speed =Time/Distance.
Now, we can use dimensional analysis to check whether this equation is correct or not.
By reducing both sides of the equation in its fundamental units form, we get
(i) [L][T]-¹ = [L] / [T] (Right)
(ii) [L][T]-¹ = [T] / [L] (Wrong)
From the above example it is evident that the dimensional formula establishes the correctness of an equation.



