Question

A ladder has rungs 25 cm apart. (see Fig. 5.7). The rungs decrease uniformly in length from 45 cm at the bottom to 25 cm at the top. If the top and the bottom rungs are \(2\frac 12\) m apart, what is the length of the wood required for the rungs?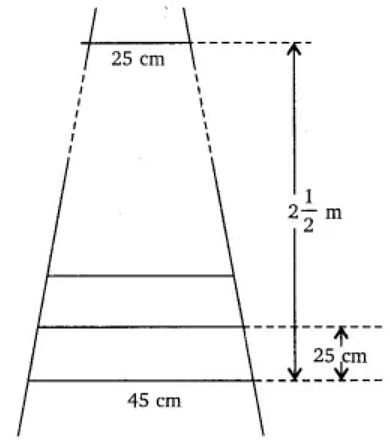

Fig. 5.7

Answer 1

It is given that the rungs are 25 cm apart and the top and bottom rungs are \(2\frac 12\) m apart.
∴ Total number of rungs = \(\frac {2\frac 12  \times 100}{25} +1 = \frac {250}{25} + 1 = 11\)
Now, as the lengths of the rungs decrease uniformly, they will be in an A.P.
The length of the wood required for the rungs equals the sum of all the terms of this A.P. 
First term, \(a = 45\)
Last term, \(l = 25\) and \(n = 11\)
\(S_n = \frac n2(a+l)\)
\(S_{10} = \frac {11}{2}(45+25)\)
\(S_{10}= \frac {11}{2} (70)\)
\(S_{10}= 385\) cm
Therefore, the length of wood is 385cm.